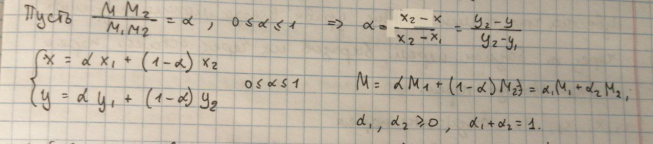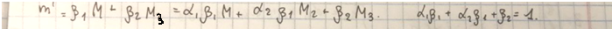Выпуклые множества теорема решение задачи линейного программирования

Множества решений неравенств, уравнений и их систем в задачах линейного программирования.

Множеством решений неравенств, уравнений и их систем на плоскости Ox₁x₂ является многоугольник решений – выпуклое многоугольное множество, образованное линиями из системы ограничений или из самих неравенства, уравнения.

Многоугольник решений может быть не ограничен сверху и/или снизу.

Иногда многоугольник может принять вид полуплоскости или даже отрезка прямой.

Если n – m = 2, где n – количество переменных, m – количество уравнений, то решение задачи можно показать на плоскости.

Теорема: Множество допустимых решений системы 2 х m линейных неравенств с n переменными является выпуклым n–мерным многогранником (выпуклой n–мерной многогранной областью).

Допустимые решения.

Теорема 1: Область допустимых решений задачи линейного программирования является выпуклым множеством.

Теорема 2: Множество допустимых решений системы с m линейных неравенств с n переменными является выпуклым n–мерным многогранником (выпуклой n–мерной многогранной областью).

Теорема 3: Если задача имеет оптимальное решение, то целевая функция принимает минимальное (максимальное) значение в одной из угловых точек многогранника допустимых решений.

Этот многогранник можно получить из системы ограничений.

Допустимые базисные решения.

Теорема : Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника допустимых решений, и наоборот, каждой угловой точке многогранника допустимых решений соответствует допустимое базисное решение задачи.

Сведения из теории выпуклых множеств.

Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.

Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.

Граничные точки множества образуют его границу.

Множество называется замкнутым, если оно содержит все свои граничные точки.

Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.

Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.

Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.

Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.

Выпуклые множества в n-мерном пространстве.

Рассмотрим двумерный случай (n = 2)

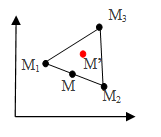
Пусть у нас есть четыре точки: M₁, M₂, M₃, M

Координаты M можно записать через координаты точек, на отрезке

между которыми она находится:

M₁, M₂, M₃ – треугольник, а любой треугольник это выпуклое множество.

Пусть точка M’ лежит на отрезке M; M₃. Тогда её координаты можно записать следующим образом:

Так при помощи M₁, M₂, M₃ можно записать любую M’ в множестве.

Тогда выпуклым множеством в n-мерном пространстве является любая линейная комбинация вида

Источник

2.4. Основные теоремы линейного программирования

Приведем без доказательства некоторые теоремы линейного программирования, которые будут полезны для нас в дальнейшем при построении линейных оптимизационных моделей.

Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Определение. Множество точек (область) является выпуклым, если оно, вместе с любыми двумя своими точками, содержит в себе отрезок, соединяющий эти точки.

На рис. 2.1 а) и рис. 2.1 б) показаны примеры выпуклых множеств, а на рис. 2.1 в) – пример множества точек, которое не является выпуклым.

Рис. 2.1. Примеры выпуклых множеств точек (а и б) и невыпуклого множества точек (в)

Теорема 2. Если задача линейного программирования имеет оптимальный план (решение), то он обязательно находится в одной из вершин ее области допустимых решений. Если же целевая функция принимает экстремального значения более чем в одной вершине многогранника области допустимых решений, то она достигает его и в любой точке, являющейся линейной комбинацией таких вершин (такие вершины будут на многограннике соседними).

Определение. Непустое множество планов основной задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений – вершиной.

Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника области допустимых решений.

Теорема 4. Каждой угловой точке множества допустимых решений соответствует допустимое базисное решение.

Теорема 5. Любая система из k векторов n-мерного векторного пространства при k < n является линейно зависимой.

Глава 3. Графический метод решения задач линейной оптимизации

3.1. Геометрическая интерпретация задачи линейного программирования

3.2. Пример использования графического метода

3.3. Частные случаи использования графического метода

3.4. Общий алгоритм графического метода

3.1. Геометрическая интерпретация задачи линейного программирования

Для представления задачи линейного программирования в геометрической форме для каждого i-го ограничения в n-мерном пространстве задается полуплоскость (или гиперплоскость) решений. В результате пересечения всех полуплоскостей, определяемых ограничениями, образуется выпуклый многогранник допустимых решений.

Целевую функцию в n-мерном пространстве геометрически можно интерпретировать как семейство параллельных полуплоскостей, положение каждой из которых определяется значением параметра F.

Задача состоит в том, чтобы найти такую точку многогранника решений, в которой целевая функция принимает максимальное или минимальное значение.

На рис. 3.1 показано геометрическое представление некоторой задачи линейного программирования в двумерном пространстве с четырьмя ограничениями и целевой функцией вида . Выпуклым многогранником допустимых решений является многогранник ABCDE. Координаты любой его точки удовлетворяют как систему ограничений, так и условие неотрицательности переменных, поскольку он находится в первой координатной полуплоскости.

В том случае, если в системе ограничений будет не две, а три переменных, то каждое ограничение геометрически будет определяться гиперполуплоскостью трехмерного пространства. Если же в системе ограничений количество переменных больше, чем три (х₁, х₂,… х_n), то каждое ограничение определяет гиперполуплоскость n-мерного пространства.

Заметим что, если область допустимых решений неограниченна, то минимум или максимум линейной функции может и не достигаться.

Рис. 3.1. Геометрическая форма представления задачи линейного программирования

Источник