Вектор градиент при решении задачи линейного программирования

Графический (геометрический) метод решения задач ЛП

Пример 5.1. Решить следующую задачу линейного программирования геометрическим методом:

Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.

1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).

Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):

Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х₂ через х₁:

Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 5.1). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из неравенств системы ограничений.

Определим полуплоскости – решения каждого из неравенств.

Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:

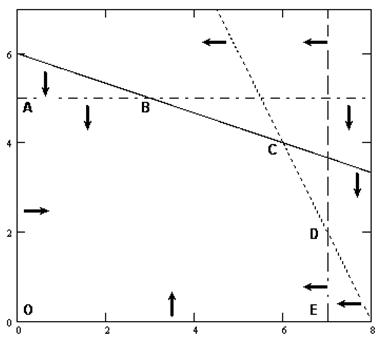
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 5.1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I)[1].

Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:

3 этап: определение ОДР задачи линейного программирования.

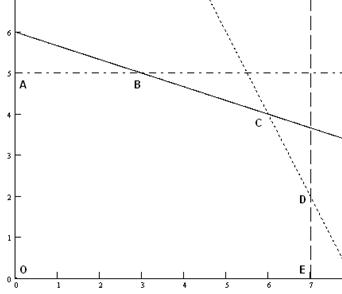
Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.

Рис. 5.1. Область допустимых решений задачи

4 этап: построение вектора-градиента.

Вектор-градиент показывает направление максимизации целевой функции[2]. Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:

Построим данный вектор на графике (рис. 5.2).

5 этап: построение прямой целевой функции.

Рассмотрим целевую функцию данной задачи:

Зададим ей какое-либо значение, к примеру, . Выразим переменную х₂ через х₁:

Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:

Построим прямую соответствующую целевой функции (рис. 5.2).

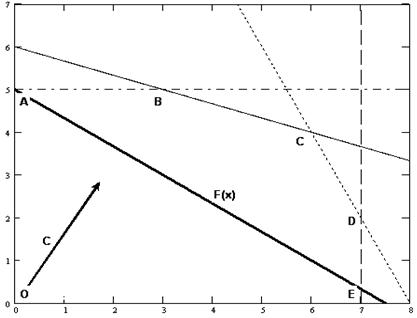
Рис. 5.2. Построение целевой функции F(X) и вектора-градиента С

6 этап: определение максимума целевой функции.

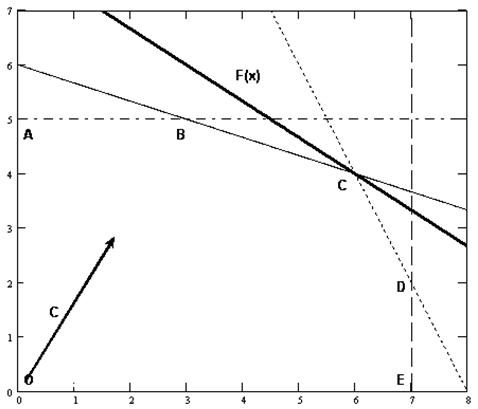
Перемещая прямую F(X) параллельно самой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.3), такой точкой является точка С ­– точка пересечения прямых I и II.

Рис. 5.3. Определение точки максимума целевой функции F(X)

Определим координаты точки С, с этой целью, решим следующую систему линейных уравнений:

Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:

Ответ: при заданных ограничениях максимальное значение целевой функции F (Х)=24, которое достигается в точке С, координаты которой х₁ =6, х₂ =4.

Пример 5.2. Решить задачу линейного программирования геометрическим методом:

Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.

4 этап: построение вектора-градиента.

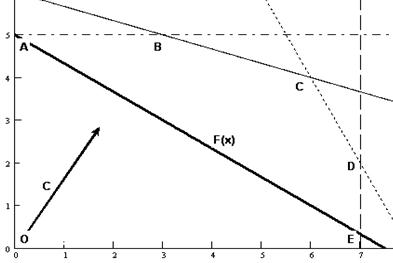
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 5.4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функции F (X).

5 этап: построение прямой целевой функции.

Построение прямой целевой функции F (X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 5.4).

Рис. 5.4. Построение целевой функции F(x) и вектора-градиента С

6 этап: определение оптимума целевой функции.

Перемещая прямую F(x) параллельно самой себе в направлении, обратном вектору-градиенту, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.5), такой точкой является точка О с координатами (0; 0).

Рис. 5.5. Определение точки минимума целевой функции

Подставляя координаты точки минимума в целевую функцию, определяем ее оптимальное (минимальное) значение, которое равно 0.

Ответ: при заданных ограничениях минимальное значение целевой функции F (Х)=0, которое достигается в точке О (0; 0).

Пример 5.3. Решить следующую задачу линейного программирования геометрическим методом:

Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x₁ и x₂.

Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные x₁ и x₂.

Умножим (поэлементно) первую строку на –3 и сложим со второй:

Сложим вторую с первой строкой:

В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

Запишем полученную задачу линейного программирования

Так как переменные x₁ и x₂ неотрицательные, то полученную систему ограничений можно записать в следующем виде:

Тогда исходную задачу можно записать в виде следующей эквивалентной ей стандартной задаче линейного программирования:

Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.

1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).

Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):

Построим прямые, соответствующие каждому неравенству (рис. 5.6). Прямые пронумеруем согласно принятой ранее схеме.

2 этап: определение решения каждого из неравенств системы ограничений.

С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 5.6) с помощью стрелок.

3 этап: определение ОДР задачи линейного программирования.

Найденные полуплоскости (решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.

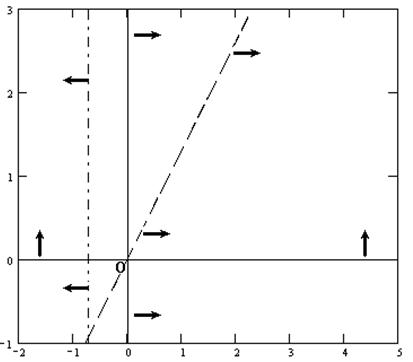
Рис. 5.6. Фрагмент MathCAD-документа:

построение области допустимых решений задачи

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Графический метод решения ЗЛП

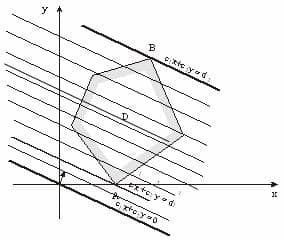
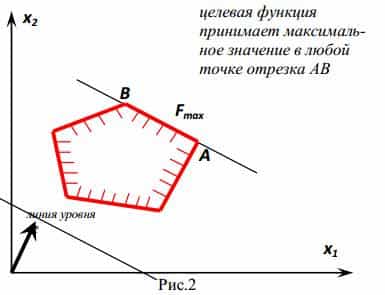
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

Инструкция . Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x₁ ≤ 4 , то оно разбивается на два: x₁ ≥ 1 , x₁ ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.

Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.
6. Вычисляют координаты точки и значение целевой функции в этой точке.

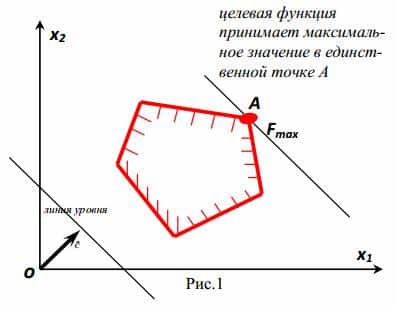
Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.

1. Сформулировать математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования графическим способом (для двух переменных).

Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

Особенности решения задач линейного программирования графическим методом

Переменную x₂ принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x₁ + 6x₃+ 27
x₁ + 3x₃≥6

Далее задача решается графическом способом.

Пример №2
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅ → max при ограничениях:
x₁ + x₂ + x₃=12
2x₁ — x₂ + x₄=8
— 2x₁ + 2x₂ + x₅=10
F(X) = 3x₁ — 2x₂ + 5x₃ — 4x₅
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

1	1	1	0	0	12
2	-1	0	1	0	8
-2	2	0	0	1	10

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₃.
2. В качестве базовой переменной можно выбрать x₄.
3. В качестве базовой переменной можно выбрать x₅.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x₁ + x₂ + x₃ = 12
2x₁ — x₂ + x₄ = 8
— 2x₁ + 2x₂ + x₅ = 10
Выразим базисные переменные через остальные:
x₃ = — x₁ — x₂+12
x₄ = — 2x₁ + x₂+8
x₅ = 2x₁ — 2x₂+10
Подставим их в целевую функцию:
F(X) = 3x₁ — 2x₂ + 5(- x₁ — x₂+12) — 4(2x₁ — 2x₂+10)
или
F(X) = — 10x₁ + x₂+20 → max
Система неравенств:
— x₁ — x₂+12 ≥ 0
— 2x₁ + x₂+8 ≥ 0
2x₁ — 2x₂+10 ≥ 0
Приводим систему неравенств к следующему виду:
x₁ + x₂ ≤ 12
2x₁ — x₂ ≤ 8
— 2x₁ + 2x₂ ≤ 10
F(X) = — 10x₁ + x₂+20 → max

• Составить систему математических зависимостей (неравенств) и целевую функцию.
• Изобразить геометрическую интерпретацию задачи.
• Найти оптимальное решение.
• Провести аналитическую проверку.
• Определить существенные и несущественные ресурсы и их избытки.
• Определить значение целевой функции.
• Вычислить объективно обусловленные оценки.
• Составить соотношение устойчивости.

Источник