Симплексный метод решения задач линейного программирования
Симплексный метод – это метод последовательного улучшения плана. Этим методом можно решать задачи линейного программирования с любым количеством переменных и ограничений.
Этот метод включает в себя три основные этапа:
- Построение начального опорного плана.
- Правило перехода к лучшему (точнее, нехудшему) решению.
- Критерий проверки найденного решения на оптимальность.
1) Построение начального опорного плана.
Данную задачу линейного программирования необходимо сначала привести к каноническому виду; при этом правые части ограничений должны быть неотрицательными. Признаком возможности построения начального опорного плана служит наличие в каждом ограничении-равенстве с неотрицательной правой частью базисной переменной. Базисной называют плановую переменную, которая входит только в одно уравнение (а в другие не входит), и при этом имеет коэффициент, равный единице. Пусть задача линейного программирования приведена к каноническому виду, и все уравнения системы ограничений имеют свою базисную переменную. Приравняв базисные переменные к соответствующим правым частям ограничений, а остальные переменные к нулю, получим опорное или базисное решение задачи. Пример. Для данной задачи линейного программирования найти начальный опорный план (базисное решение). 


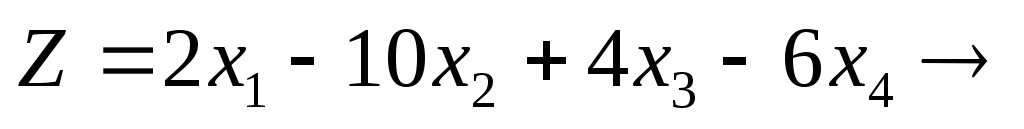
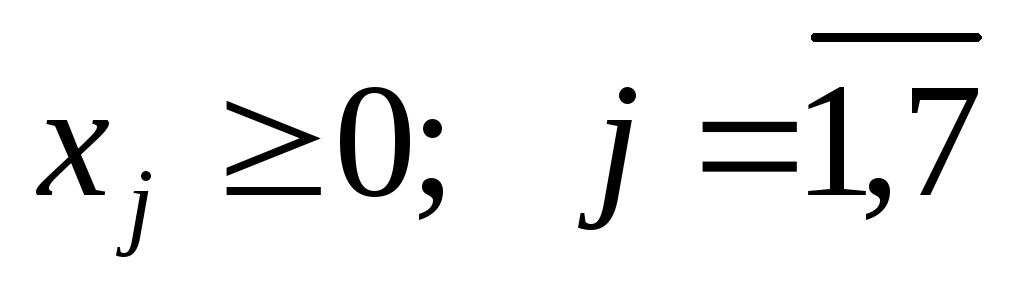




2) Составление симплексных таблиц. Критерий оптимальности.
Симплексный метод удобно применять, используя построение симплексных таблиц. Первая симплексная таблица, соответствующая начальному плану, имеет вид:
| Базис | 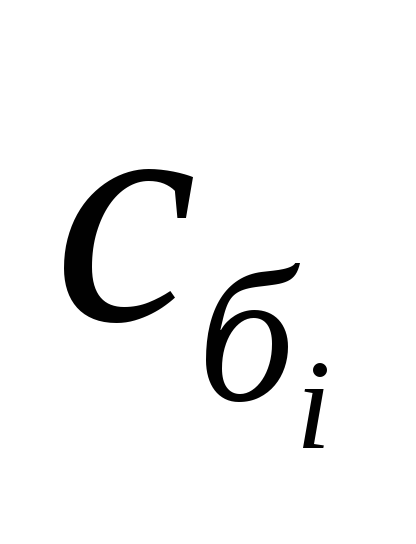 | В |  |  | … |  |  |
 | 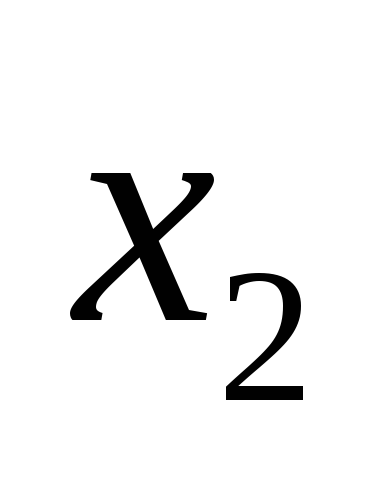 | … | 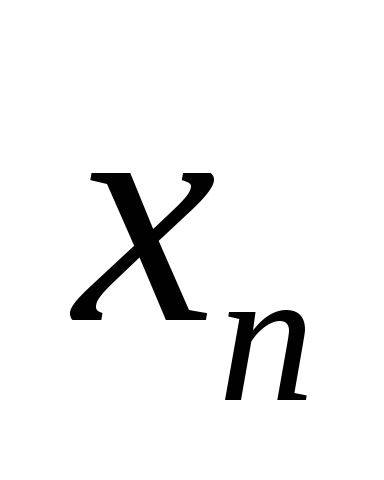 | ||||
 |  |  |  |  | … |  | |
 |  | 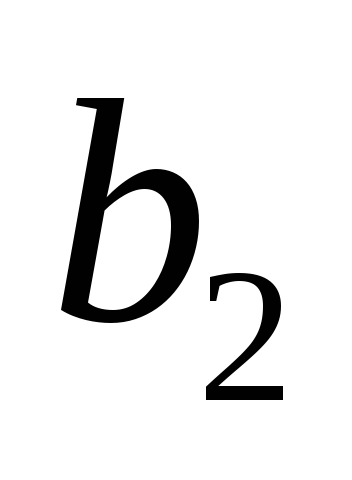 |  | 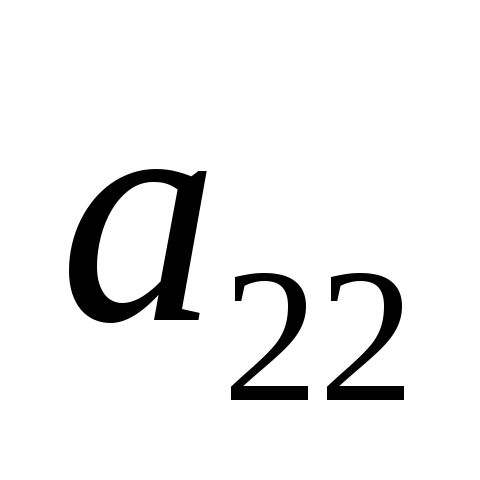 | … |  | |
| … | … | … | … | … | … | … | |
 | 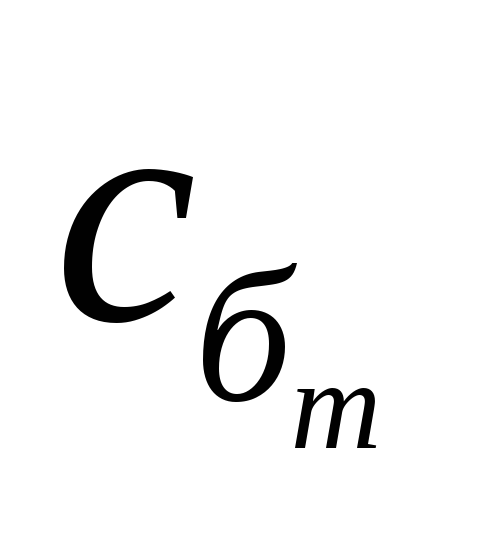 | 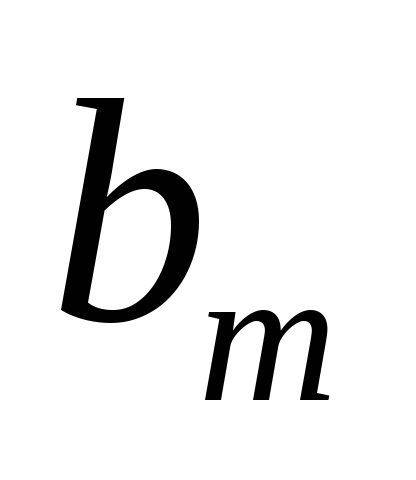 |  |  | … | 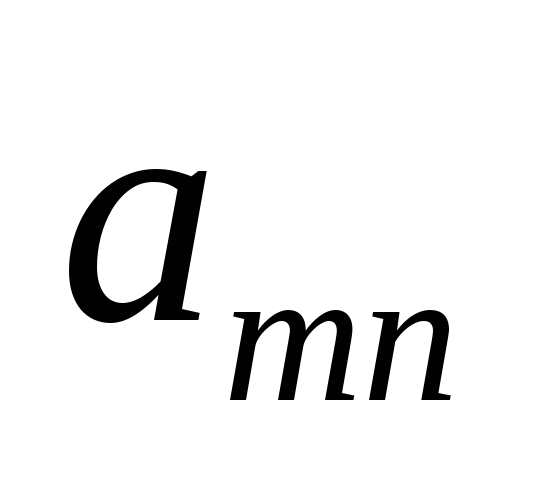 | |
 |  |  |  | … |  | ||
Здесь приняты следующие обозначения. Столбец «Базис» – это базисные переменные. Столбец «









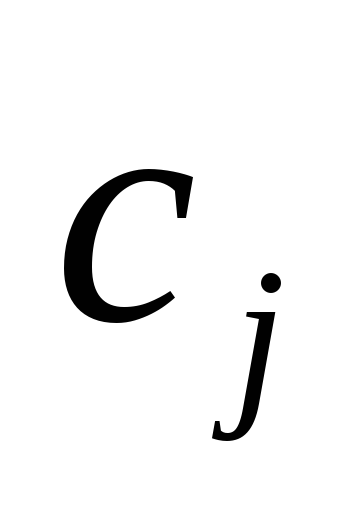










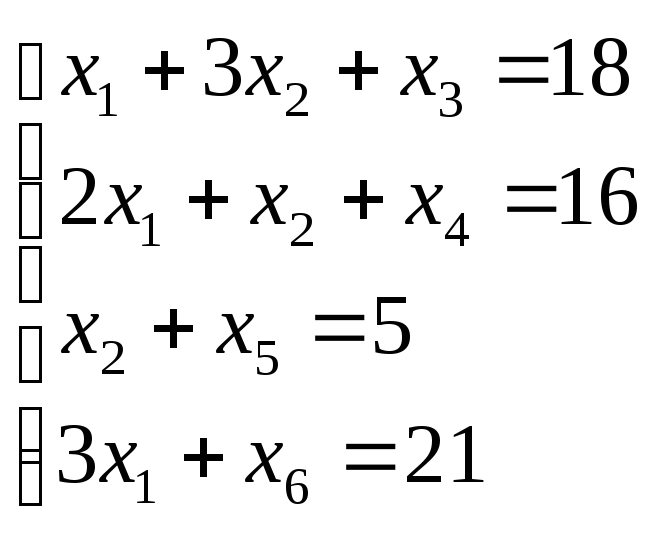



| Базис | 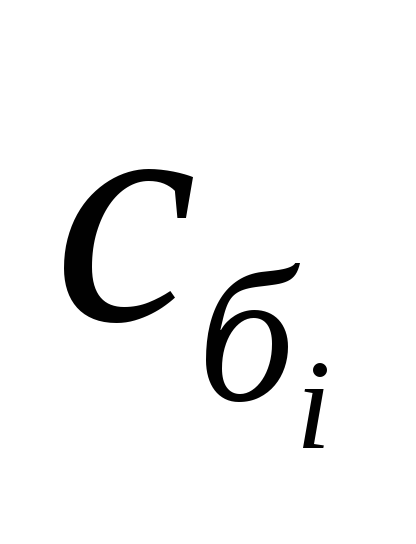 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 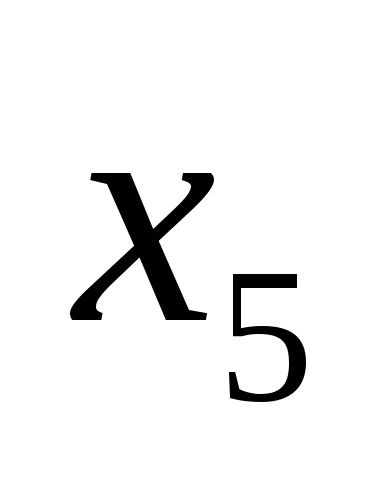 |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 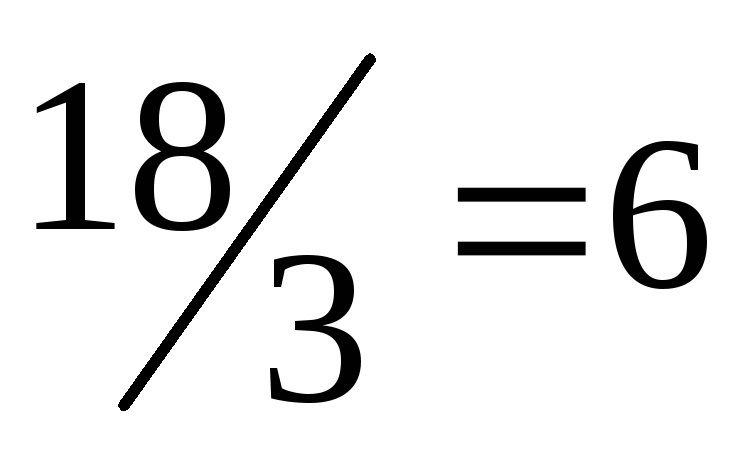 |
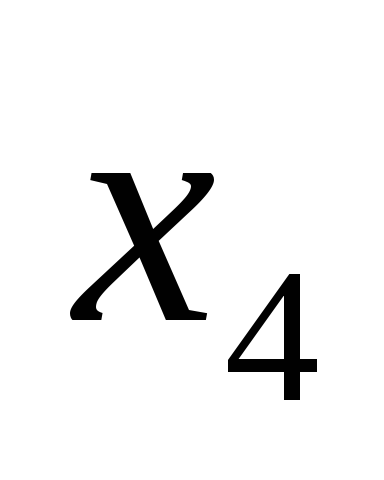 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 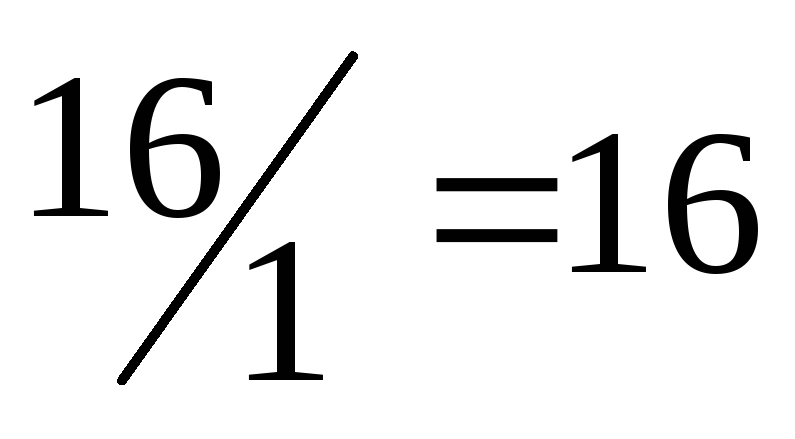 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 |  |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 |  0 0 |  –2 –2 |  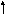 –3 –3 |  0 0 |  0 0 |  0 0 |  0 0 | ||
Здесь 






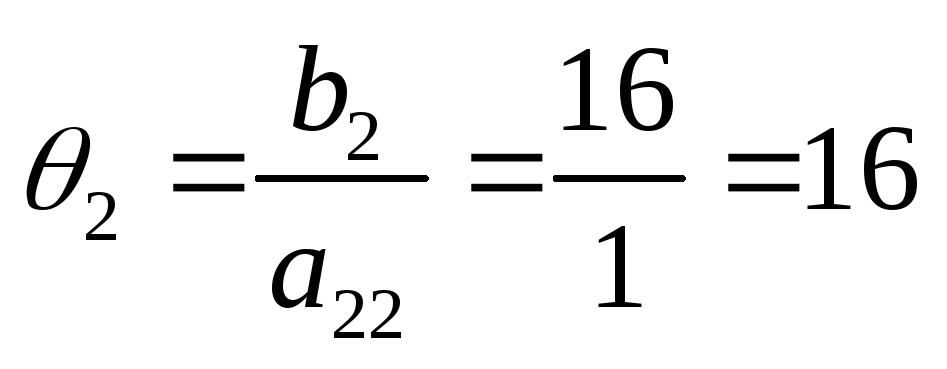

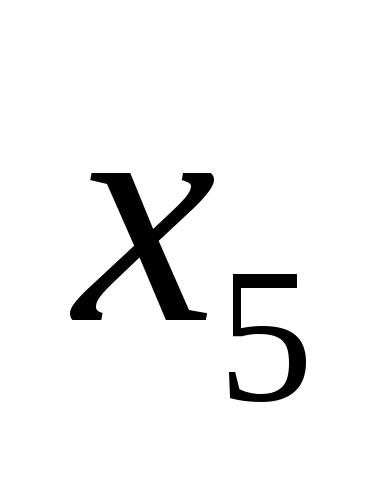
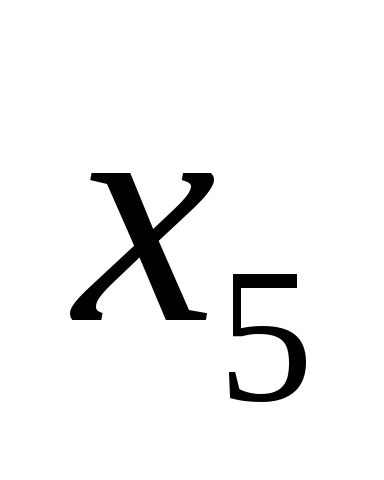

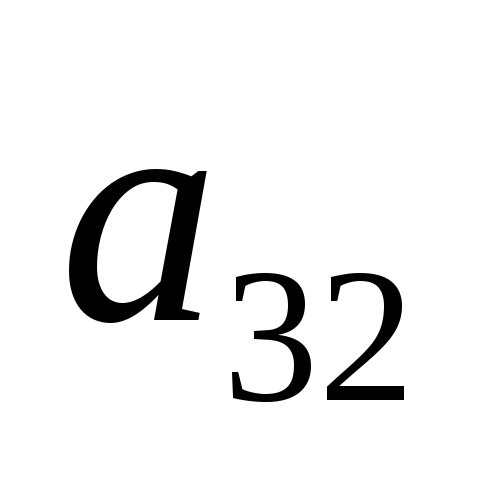
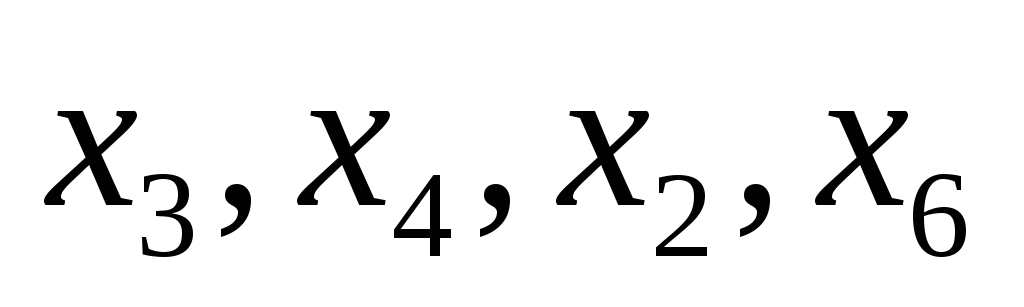




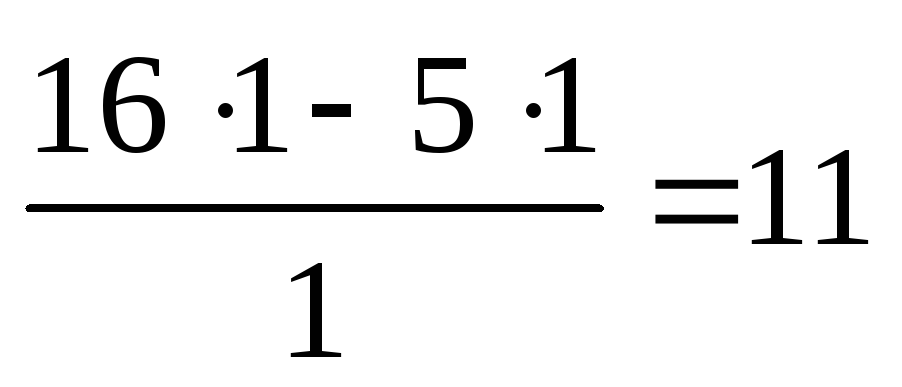



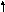
| Базис | 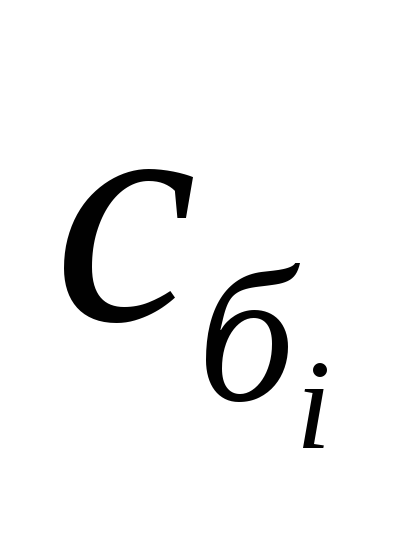 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 | 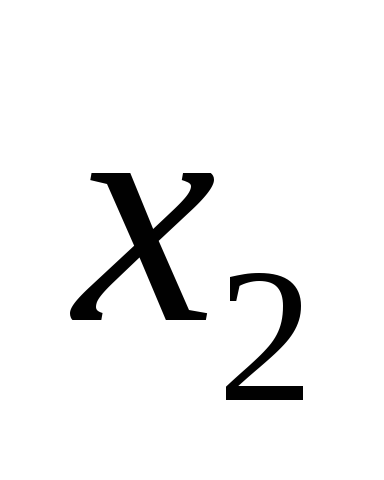 | 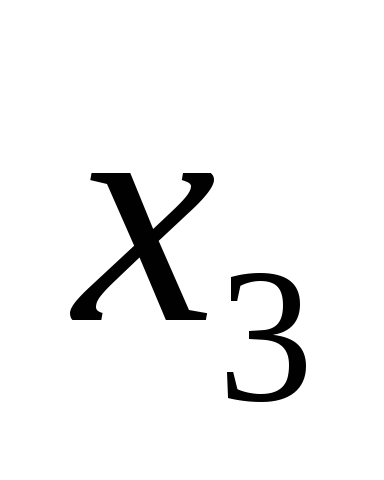 |  |  |  | ||||
 | 0 | 18 | 1 | 3 | 1 | 0 | 0 | 0 | 6 |
 | 0 | 16 | 2 | 1 | 0 | 1 | 0 | 0 | 16 |
 | 0 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | – |
 | 0 | –2 | –3 | 0 | 0 | 0 | 0 | таб. 1 | |
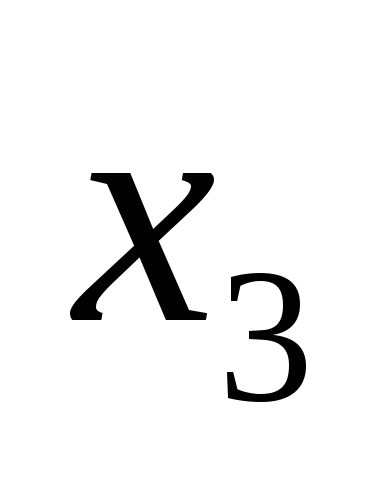 | 0 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | 3 |
 | 0 | 11 | 2 | 0 | 0 | 1 | –1 | 0 | 5,5 |
 | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | – |
 | 0 | 21 | 3 | 0 | 0 | 0 | 0 | 1 | 7 |
 | 15 | –2 | 0 | 0 | 0 | 3 | 0 | таб. 2 | |
| Базис | 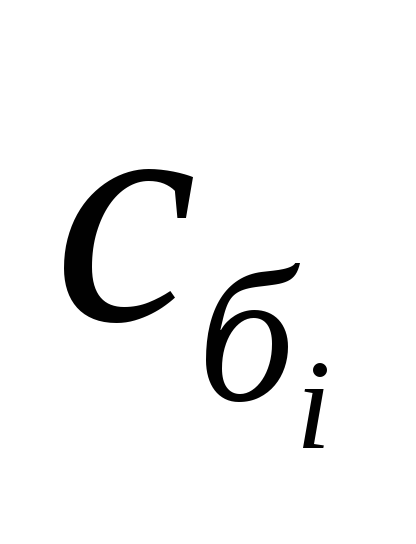 | В | 2 | 3 | 0 | 0 | 0 | 0 |  |
 |  |  |  | 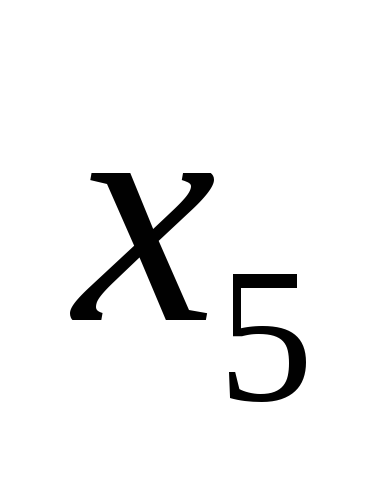 |  | ||||
 | 2 | 3 | 1 | 0 | 1 | 0 | –3 | 0 | – |
 | 0 | 5 | 0 | 0 | –2 | 1 | 5 | 0 | 1 |
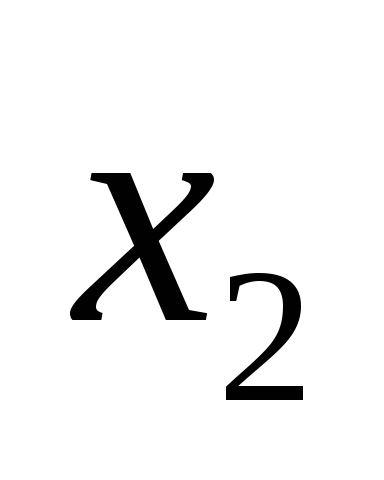  | 3 | 5 | 0 | 1 | 0 | 0 | 1 | 0 | 5 |
 | 0 | 12 | 0 | 0 | –3 | 0 | 9 | 1 |  |
 | 21 | 0 | 0 | 2 | 0 | –3 | 0 | таб. 3 | |
 | 2 | 6 | 1 | 0 | –0,2 | 0,6 | 0 | 0 | |
 | 0 | 1 | 0 | 0 | –0,4 | 0,2 | 1 | 0 | |
 | 3 | 4 | 0 | 1 | 0,4 | –0,2 | 0 | 0 | |
 | 0 | 3 | 0 | 0 | 0,6 | –1,8 | 0 | 1 | |
 | 24 | 0 | 0 | 0,8 | 0,6 | 0 | 0 | таб. 4 | |
О













| а) | 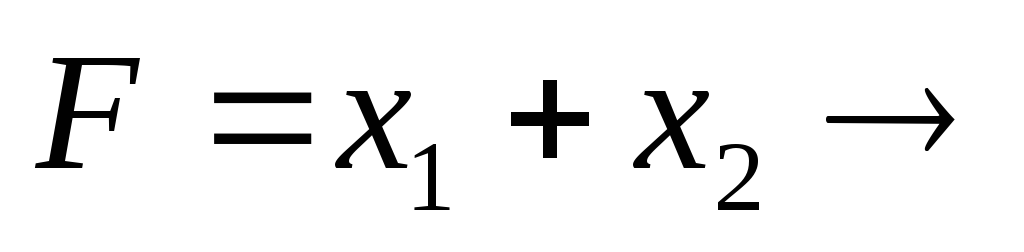 max max 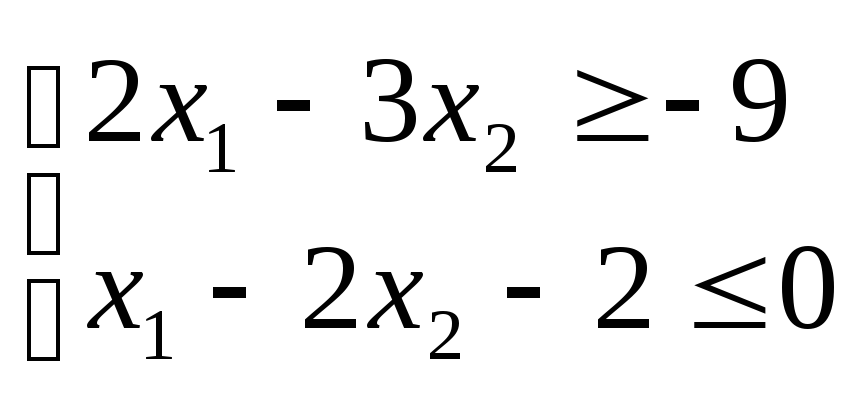 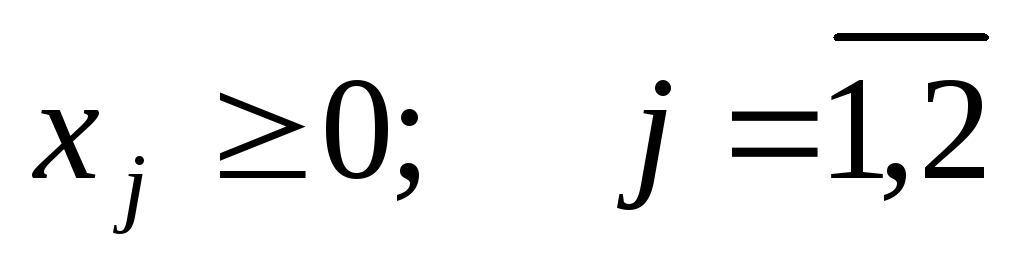 | б) |  min min   |
Тема 3. Симплексный метод решения задач линейного программирования
Суть симплекс-метода заключается в том, что решение ЗЛП осуществляется итерационно и основывается на переходе от одного допустимого базисного решения к другому, при котором значение целевой функции улучшается. Этот процесс длится до тех пор, пока дальнейшее улучшение целевой функции станет невозможно.
В алгебраических терминах симплекс-метод предполагает:
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника ОДР к соседней, в которой целевая функция принимает лучшее значение, до тех пор, пока не будет найдено оптимальное решение.
Симплексный метод универсален, поскольку позволяет решить любую ЗЛП.
2. Критерий оптимальности решения злп
Для использования симплекс-метода ЗЛП должна быть приведена к каноническому виду с предпочтительными переменными.
Критерий оптимальности. Решение ЗЛП является оптимальным, если неотрицательны коэффициенты целевой функции при переменных, имеющих определенный смысл (экономический, технологический, физический), и все свободные члены в правой части уравнений системы ограничений ( ).
В ходе решения ЗЛП могут возникнуть 4 случая:
1) , следовательно, план не оптимален и используется основной симплекс-метод;
2) , следовательно, план не оптимален и применяется двойственный симплекс-метод;
3) , следовательно, план не оптимален и применяется смешанный симплекс-метод;
4) , следовательно, согласно критерию оптимальности, план оптимален.
3. Алгоритм основного симплекс-метода:
1) Записать математическую модель в допустимом предпочтительном виде канонической формы.
2) Составить нулевую итерацию, записав математическую модель ЗЛП в первую симплекс-таблицу и взяв в качестве базисных переменных предпочтительные.
3) При наличии отрицательных коэффициентов целевой функции сj осуществить подготовку к переходу к новому решению по следующей схеме:
а) среди отрицательных коэффициентов целевой функции выбрать максимальный по модулю, соответствующий столбец в симплекс-таблице называется разрешающим и помечается знаком *.
б) среди всех отношений правых частей системы ограничений к положительным элементам разрешающего столбца выбрать минимальное, соответствующая строка называется разрешающей и помечается знаком *.
в) элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, называется разрешающим и помещается в рамку .
4) Заполнить следующую симплекс-таблицу:
а) базисную переменную (б.п.) в разрешающей строке заменить на переменную разрешающего столбца, все остальные переменные оставить в неизменном порядке;
б) заполнить столбцы базисных переменных: на пересечении столбца и строки базисной переменной поставить 1, остальные элементы столбца приравнять нулю;
в) если в разрешающем столбце прежней таблицы есть 0, то соответствующую ему строку переписать без изменений;
г) если в разрешающей строке прежней таблицы есть 0, то соответствующий ему столбец переписать без изменений;
д) построить опорную строку (·) в новой таблице, разделив все элементы разрешающей строки прежней таблицы на разрешающий элемент;
е) все остальные элементы новой таблицы определяются по правилу треугольника: новый элемент равен прежнему минус произведение соответствующего по строке элемента в разрешающем столбце прежней таблицы на элемент опорной строки в столбце искомого элемента новой таблицы; исключением является элемент, стоящий на пересечении строки целевой функции и столбца свободных членов ограничений, для которого в правиле треугольника «–» следует заменить на «+».
5) Целевая функция в новой таблице проверяется на оптимальность: если при реальных переменных, то получен оптимальный план решения ЗЛП, а если среди сj есть отрицательный коэффициент, то перейти к пункту 2 алгоритма.
Задача. Для изготовления двух видов , продукции используют три вида ресурсов , , . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в технологической таблице:
Число единиц ресурсов, затрачиваемых на изготовление единицы продукции

