Решение системы нелинейных уравнений питон

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Различные алгоритмы численных методов на языке Python.

alwayswannasky/Numerical-methods

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Различные алгоритмы численных методов на языке Python.

Решение СЛАУ. Собственные значения и векторы

• 1 — Метод Гаусса
• 2 — Метод Жордана–Гаусса
• 3 — Метод LU–разложения
• 4 — Метод квадратных корней (схема Холецкого)
• 5 — Метод ортогонализации
• 6 — Метод прогонки
• 7 — Метод простых итераций
• 8 — Метод Якоби
• 9 — Обратная матрица(методом Гаусса)
• 10 — Решение СЛАУ в комплексном пространстве
• 11 — Максимальное и минимальное по модулю собственные значения и соответствующие им собственные векторы
• 12 — Переопределенные СЛАУ с помощью методов ортогонализации и минимизацией отклонений

Решение нелинейных уравнений и систем

• 1 — Метод половинного деления
• 2 — Метод Ньютона–Рафсона (касательных)
• 3 — Метод секущих (хорд)
• 4 — Комбинированный метод
• 5 — Метод простых итераций
• 6 — Метод Ньютона
• 7 — Метод спуска
• 8 — Решение линейных уравнений с помощью системы Штурма

Теория приближения и аппроксимация функций

• 1 — Интерполяционный многочлен Лагранжа для функции, заданной таблично
• 2 — Интерполяционный многочлен Лагранжа для заданной функции 𝑓(𝑥) с заданными узлами. Погрешность интерполяции
• 3 — Интерполяционный многочлен Ньютона для функции, заданной таблично
• 4 — Интерполяционный многочлен Ньютона для заданной функции 𝑓(𝑥) с заданными узлами. Погрешность интерполяции
• 5 — Интерполяционный многочлен Эрмита
• 6 — Интерполяционный кубический сплайн для функции из 1)
• 7 — Интерполяционный кубический сплайн для функции из 2)
• 8 — Метод наименьших квадратов, прямая линейной регрессии, аппроксимирующаю функцию, заданную таблично

• 1 — Создание таблицы с приближенными значениями производной функции 𝑓′(𝑥), используя формулы первого порядка точности
• 2 — Создание таблицs с приближенными значениями первой производной функции 𝑓′(𝑥), используя формулы второго порядка точности
• 3 — Создание таблицы приближенных значений производных функции 𝑓′′(𝑥), вычисляемых по формулам второго порядка точности
• 4 — Производные первого и второго порядков, используя интерполяционный метод
• 5 — Вычисление производных первого и второго порядков при помощи сплайнов

• 1 — Формулы прямоугольников
• 2 — Формула трапеций
• 3 — Формула Симпсона
• 4 — Формулы интерполяционного типа
• 5 — Формула Гаусса
• 6 — Первый интеграл с помощью сплайнов
• 7 — Метод Рунге–Ромберга
• 8 — Несобственный интеграл

Численное решение задачи Коши

• 1 — Метод последовательных приближений
• 2 — Метод Эйлера, его модификации
• 3 — Метод Рунге-Кутта
• 4 — Метод Адамса
• 5 — Метод Рунге-Ромберга в правом конце отрезка

Нахождение точек пересечения куба с плоскостью.

About

Различные алгоритмы численных методов на языке Python.

Источник

Решение нелинейных уравнений#

Подмодуль scipy.optimize также содержит в себе методы для поиска корней нелинейных уравнений и их систем.

from matplotlib import pyplot as plt def configure_matplotlib(): plt.rc('text', usetex=True) plt.rcParams["axes.titlesize"] = 28 plt.rcParams["axes.labelsize"] = 24 plt.rcParams["legend.fontsize"] = 24 plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18 plt.rcParams["text.latex.preamble"] = r""" \usepackage[utf8]  \usepackage[english,russian]  \usepackage  """ configure_matplotlib() 

Поиск корня скалярной функции одного аргумента#

Функция scipy.optimize.root_scalar позволяет искать корни функции \(f\colon \mathbb \to \mathbb\) :

Функция root_scalar предоставляет доступ к разным методам поиска корней, таким как newton , bisect , secant и многим другим. Какие-то из этих методов ищут корень внутри отрезка bracket , а другие ищут корень, начиная с какого-то начального приближения x0 .

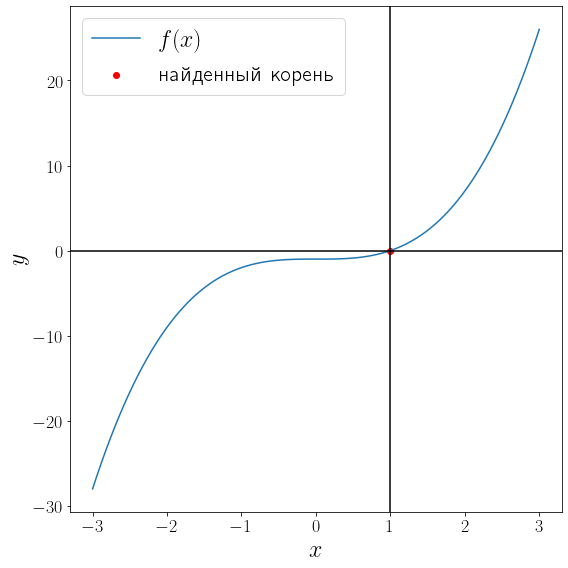
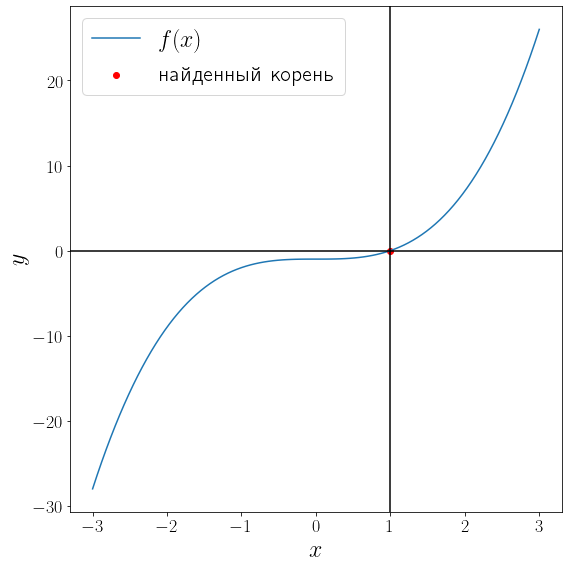
import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): return x**3 - 1 solution = optimize.root_scalar(f, bracket=[-10, 10], method="bisect") print(solution) x = np.linspace(-3, 3, 100) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() 

converged: True flag: 'converged' function_calls: 46 iterations: 44 root: 1.0000000000002274

Метод бисекции сошелся за 44 итерации. Проверим метод Ньютона.

def fprime(x): return 3 * x**2 solution = optimize.root_scalar(f, fprime=fprime, x0=-2, method="newton") print(solution) fig, ax = plt.subplots(figsize=(8, 8), layout="tight") ax.plot(x, f(x), label="$f(x)$") ax.scatter(solution.root, f(solution.root) , color="red", label="найденный корень") ax.axvline(solution.root, color="black") ax.axhline(0, color="black") ax.set_xlabel("$x$") ax.set_ylabel("$y$") ax.legend() 

converged: True flag: 'converged' function_calls: 20 iterations: 10 root: 1.0

Метод Ньютона сошелся за 11 итераций.

Решение системы нелинейных уравнений.#

Функция optimize.root предназначена для поиска корней уравнений вида

где \(x\in\mathbb^n\) и \(F\colon \mathbb^n \to \mathbb^n\) многомерны, т.е. optimize.root решает системы вида

Рассмотрим поиск корня на примере функции

Матрица Якоби этого уравнения имеет вид

\[\begin \begin 1 + \frac(x_2 — x_1)^2 & \frac(x_2 — x_1)^2 \\ \frac(x_2 — x_1)^2 & 1 + \frac(x_2 — x_1)^2 \end, \end\]

а единственный действительный корень которой

В самом простом варианте достаточно передать методу optimize.root функцию левой части уравнения \(F\) и начальное приближение к корню.

import numpy as np from scipy import optimize from matplotlib import pyplot as plt def f(x): x = np.array(x) return np.array([ x[0] + 0.5 * (x[0] - x[1])**3 - 1.0, 0.5 * (x[1] - x[0])**3 + x[1] - 1.0 ]) solution = optimize.root(f, x0 = [0, 0]) print(solution) 

fjac: array([[-1.00000000e+00, -1.09073861e-12], [ 1.09073861e-12, -1.00000000e+00]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 5 qtf: array([-2.18114415e-12, -2.18114415e-12]) r: array([-1.00000000e+00, -2.18119967e-12, -1.00000000e+00]) status: 1 success: True x: array([1., 1.])

Если известно аналитическое выражение для производно, то лучше задействовать его и передать по параметру jac .

def jac(x): return np.array([ [1 + 1.5 * (x[0] - x[1])**2, -1.5 * (x[0] - x[1])**2], [-1.5 * (x[1] - x[0])**2, 1 + 1.5 * (x[1] - x[0])**2] ]) solution = optimize.root(f, jac=jac, x0 = [0, 0], method="hybr") print(solution) 

fjac: array([[-1., 0.], [ 0., -1.]]) fun: array([0., 0.]) message: 'The solution converged.' nfev: 2 njev: 1 qtf: array([1., 1.]) r: array([-1., -0., -1.]) status: 1 success: True x: array([1., 1.])

Источник

Метод Ньютона, решение нелинейных уравнений на Python

Метод Ньютона, также известный как метод касательных, является численным методом для нахождения корня нелинейного уравнения. Он основан на идее использования локального линейного приближения функции в окрестности предполагаемого корня для последующего уточнения его координат.

Алгоритм метода Ньютона для решения нелинейных уравнений

Процесс решения нелинейного уравнения методом Ньютона состоит из следующих шагов:

1. Задать начальное приближение корня x0.
2. Выразить функцию f(x) в виде локального линейного приближения в окрестности x0, используя формулу Тейлора: f(x) ≈ f(x0) + f'(x0) * (x – x0)
3. Решить полученное линейное уравнение относительно x, положив его равным нулю: 0 = f(x0) + f'(x0) * (x – x0)
4. Вычислить новое приближение корня, используя полученное решение: x1 = x0 – f(x0) / f'(x0)
5. Повторять шаги 2-4, пока не будет достигнута необходимая точность или заданное количество итераций.

Преимущества и недостатки метода Ньютона

Заметим, что метод Ньютона может сходиться к корню очень быстро, если начальное приближение близко к корню и функция имеет достаточно гладкую поверхность. Однако, если начальное приближение далеко от корня или функция имеет слишком сложную поверхность, метод может сходиться очень медленно или даже расходиться. Также важно учитывать, что метод Ньютона может находить только один корень в заданной окрестности начального приближения.

Пошаговая реализация метода Ньютона на Python

• Определение функции newton_method , которая принимает на вход функцию f , её производную df , начальное приближение x0 , допустимую погрешность tol и максимальное число итераций max_iter . Функция решает нелинейное уравнение f(x) = 0 с помощью метода Ньютона.

def newton_method(f, df, x0, tol=1e-6, max_iter=100):

• В теле функции newton_method создается переменная x , которая инициализируется значением начального приближения x0 .

• В цикле for выполняются итерации метода Ньютона. Цикл будет продолжаться до тех пор, пока не будет достигнута максимальная допустимая погрешность tol или не будет достигнуто максимальное число итераций max_iter .

• Затем проверяется, достигнута ли требуемая точность. Если значение fx меньше, чем tol , значит, мы нашли корень уравнения, и функция возвращает значение x и число итераций i .

• Если требуемая точность не достигнута, то вычисляется производная df в точке x и сохраняется в переменной dfx .

• Затем проверяется, равна ли производная dfx нулю. Если равна, значит, мы не можем продолжать итерации, и функция возвращает None и число итераций i .

• Если производная dfx не равна нулю, то вычисляется новое значение x с помощью формулы метода Ньютона: x = x — fx / dfx .

• Цикл завершается, и если мы не нашли корень уравнения, то функция возвращает None и число итераций i .

Метод Ньютона, готовый код

import math def newton_method(f, df, x0, tol=1e-6, max_iter=100): """ Решает нелинейное уравнение f(x) = 0 с помощью метода Ньютона. f - функция, для которой ищется корень df - производная функции f x0 - начальное приближение tol - допустимая погрешность max_iter - максимальное число итераций Возвращает корень уравнения и число итераций. """ x = x0 for i in range(max_iter): fx = f(x) if abs(fx) < tol: return x, i dfx = df(x) if dfx == 0: break x = x - fx / dfx return None, i # Пример использования функции newton_method # Решение уравнения x^2 - 2 = 0 f = lambda x: x**2 - 2 df = lambda x: 2*x x0 = 1.0 root, num_iter = newton_method(f, df, x0) if root is not None: print(f"Корень уравнения: ") print(f"Число итераций: ") else: print("Решение не найдено.")

Если функция newton_method нашла корень уравнения, то программа выводит его и число итераций. Если корень не найден, то программа выводит сообщение о том, что решение не найдено.

Результат выполнения программы в консоли:

Источник