Поправка холма бонферрони python

Notes on the Bonferroni threshold¶

The Bonferroni threshold is a family-wise error threshold. That is, it treats a set of tests as one family, and the threshold is designed to control the probability of detecting any positive tests in the family (set) of tests, if the null hypothesis is true.

Family-wise error¶

The Bonferroni correction uses a result from probability theory to estimate the probability of finding any p value below a threshold \(\theta\) , given a set (family) of \(n\) p values.

When we have found a threshold \(\theta\) that gives a probability \(\le \alpha\) that any p value will be \(\lt \theta\) , then the threshold \(\theta\) can be said to control the family-wise error rate at level \(\alpha\) .

Not the Bonferroni correction¶

The inequality used for the Bonferroni is harder to explain than a simpler but related correction, called the Šidák correction.

We will start with that, and then move on to the Bonferroni correction.

The probability that all \(n\) tests are above p value threshold \(\theta\) , assuming tests are independent:

Chance that one or more p values are \(\le \theta\) :

We want a uncorrected p value threshold \(\theta\) such that the expression above equals some desired family-wise error (FWE) rate \(\alpha_\) . For example we might want a p value threshold \(\theta\) such that there is probability ( \(\alpha_\) ) of 0.05 that there is one or more test with \(p \le \theta\) in a family of \(n\) tests, on the null hypothesis:

So, if we have 10 tests, and we want the threshold \(\theta\) to control \(\alpha_\) at \(0.05\) :

>>> def sidak_thresh(alpha_fwe, n): . return 1 - (1 - alpha_fwe)**(1./n) . >>> print(sidak_thresh(0.05, 10)) 0.0051161968918. 

The Bonferroni correction¶

\(\newcommand<\P><\mathbb P>\) The Bonferroni correction uses a result from probability theory, called Boole’s inequality. The result is by George Boole, of boolean fame. Boole’s inequality applies to the situation where we have a set of events \(A_1, A_2, A_3, \ldots \) , each with some probability of occurring \((A_1), (A_2), (A_3) \ldots \) . The inequality states that the probability of one or more of these events occurring is no greater than the sum of the probabilities of the individual events:

You can read the \(\cup\) symbol here as “or” or “union”. \(\P\biggl(\bigcup_ A_i\biggr)\) is the probability of the union of all events, and therefore the probability of one or more event occurring.

Boole’s inequality is true because:

where you can read \(\cap\) as “and” or “intersection”. Because \(P(A \cap B) \ge 0\) :

In our case we have \(n\) tests (the family of tests). Each test that we label as significant is an event. Therefore the sum of the probabilities of all possible events is \(n\theta\) . \(<\mathbb P>\biggl(\bigcup_ A_i\biggr)\) is our probability of family-wise error \(\alpha_\) . To get a threshold \(\theta\) that controls family-wise error at \(\alpha\) , we need:

For \(n=10\) tests and an \(\alpha_\) of 0.05:

>>> def bonferroni_thresh(alpha_fwe, n): . return alpha_fwe / n . >>> print(bonferroni_thresh(0.05, 10)) 0.005 

The Bonferroni correction does not assume the tests are independent.

As we have seen, Boole’s inequality relies on:

This means that the Bonferroni correction will be conservative (the threshold will be too low) when the tests are positively dependent ( \(P(A \cap B) \gg 0\) ).

The Bonferroni \(\theta_ = \alpha_ \space / \space n\) is always smaller (more conservative) than the Šidák correction \(\theta_\) for \(n \ge 1\) , but it is close:

>>> import numpy as np >>> np.set_printoptions(precision=4) # print to 4 decimal places >>> n_tests = np.arange(1, 11) # n = 1 through 10 >>> # The exact threshold for independent p values >>> print(sidak_thresh(0.05, n_tests)) [ 0.05 0.0253 0.017 0.0127 0.0102 0.0085 0.0073 0.0064 0.0057 0.0051] 

>>> # The Bonferroni threshold for the same alpha, n >>> print(bonferroni_thresh(0.05, n_tests)) [ 0.05 0.025 0.0167 0.0125 0.01 0.0083 0.0071 0.0063 0.0056 0.005 ] 

Источник

Множественные эксперименты: теория и практика

В современном мире сложно представить развитие продукта без A/B-тестирования. Чтобы успешно запустить продукт или новую функциональность — надо грамотно спроектировать A/B, рассчитать и интерпретировать его результаты. Иногда нам требуется тестирование более чем для двух групп. В этой статье мы рассмотрим как раз такой случай — множественное тестирование:

• поговорим о том, когда и зачем следует проводить множественные тесты;
• рассмотрим основные методы расчёта результатов тестов и математические принципы, на которых основаны методы;
• приведём примеры программной реализации методов; эти примеры вы сможете использовать в своих проектах.

Множественные эксперименты: когда и зачем

Очевидно, что любое техническое усложнение эксперимента должно быть обосновано практической необходимостью. Это касается и множественных тестов. Если аудитория разбивается более чем на две подгруппы, вероятность получить ошибку первого рода при эксперименте нарастает экспоненциально:

где — число подгрупп, — заданный уровень статистической значимости.
Таким образом, при добавлении всего одной дополнительной подгруппы в привычный парный тест () при заданном стандартном уровне мы получаем вероятность ошибки первого рода , что значительно превышает наш заданный .

Зачем же проводить множественные эксперименты, если они снижают точность результатов исследования? Причин может быть несколько:

1. Требуется протестировать несколько изменений и их кумулятивное воздействие на продуктовые метрики. Пример — показ пользователю на странице сервиса двух новых элементов, которые по-разному расположены относительно друг друга.
2. Изменения можно протестировать только в одном временно́м промежутке, поскольку они и взаимозависимы, и чувствительны к недельной сезонности. Пример — отключение рекламных каналов для расчёта эффекта межканальной каннибализации.
3. Заказчик хочет как можно скорее и дешевле получить ответ, какой из вариантов следует выбрать, сэкономив при этом время разработки и внедрения эксперимента.

Множественные эксперименты: особенности расчёта

Основные понятия

Рассмотрим общий случай, когда мы имеем дело с гипотезами , о попарном равенстве медианы или среднего подгрупп. В таком случае возможен и верный, и неверный результат исхода для каждой из гипотез. Представим результаты в виде confusion matrix эксперимента:

Таким образом, неверно отклонены из отклонённых основных гипотез.

Исходя из этих параметров, мы введём два важных понятия ошибок, которые контролируются при множественном тестировании: и .

Групповая вероятность ошибки (Family-Wise Error Rate) представляет собой вероятность получить по крайней мере одну ошибку первого рода и определяется формулой:

(False Discovery Rate) — это математическое ожидание отношения ошибок первого рода к общему количеству отклонений основной гипотезы:

Рассмотрим методы контроля этих ошибок на примере стандартного продуктового кейса.

Описание кейса

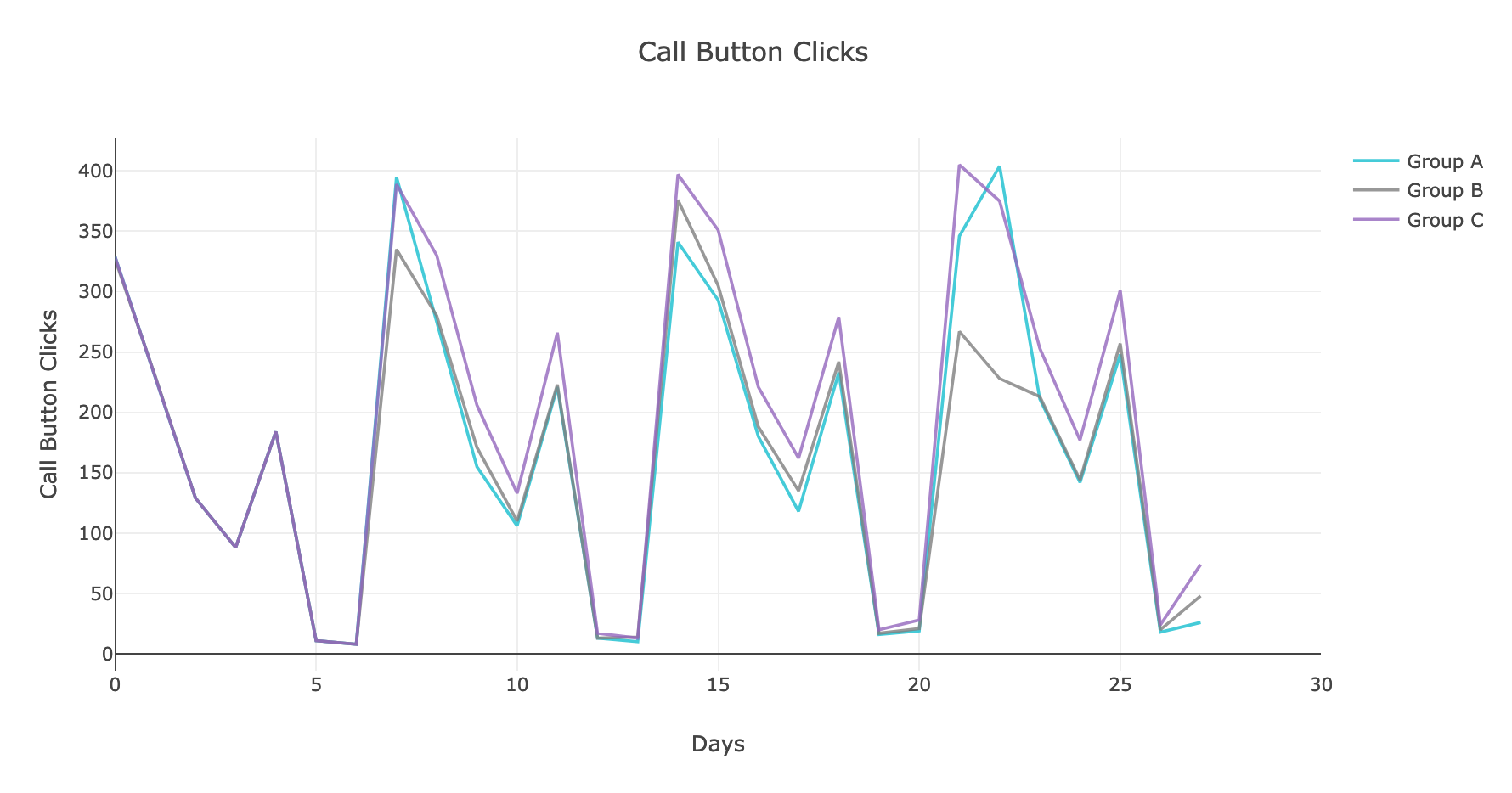
В качестве простого примера рассмотрим эксперимент, в котором трём изолированным, непересекающимся группам пользователей показали три варианта страницы с предложением нажать на кнопку звонка по объявлению. В качестве основной метрики для простоты расчёта возьмём суммарное количество звонков в каждой группе.

Посмотрим на то, как же менялась исследуемая метрика:

Рис. 1. График динамики нажатий на кнопку звонка

Воспользуемся стандартным методом , чтобы привести распределение целевой метрики в выборках к нормальному виду, и посмотрим на гистограммы и диаграммы размаха средних значений в выборках:

Рис. 2. Гистограмма распределения средних значений в группах

Рис. 3. Диаграмма размаха средних значений в группах

Судя по графикам, группа C выигрывает по количеству нажатий на кнопку звонка. Однако необходимо убедиться в статистической значимости результатов. Для этого приведём оцениваемую метрику к виду нормального распределения и воспользуемся привычным t-критерием Стьюдента для попарного сравнения групп в эксперименте, а затем — методами контроля и для учёта поправки на множественное сравнение.

Контроль FWER

Существует множество методов контроля данной ошибки, однако наиболее распространены два:

1) одношаговая процедура с одновременной корректировкой для всех тестируемых гипотез методом Бонферрони;

2) последовательная, итеративная корректировка c принятием решения на каждом шаге в соответствии с результатом методом Холма.

1. Поправка Бонферрони

Эта одношаговая процедура позволяет снизить вероятность ложноположительного результата эксперимента. Суть метода — принять альтернативную гипотезу, если:

где — количество тестируемых гипотез.

Реализовать метод можно достаточно просто при помощи стандартной библиотеки :

from bootstrapped import bootstrap as bs from bootstrapped import compare_functions as bs_cmp from bootstrapped import stats_functions as bs_st bs_ab_estims = bs.bootstrap_ab(np.array(group_A), np.array(group_B), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4) bs_bc_estims = bs.bootstrap_ab(np.array(group_B), np.array(group_C), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4) bs_ac_estims = bs.bootstrap_ab(np.array(group_A), np.array(group_C), bs_st.mean bs_cmp.difference, num_iterations=5000, alpha=0.05/3, iteration_batch_size=100, scale_test_by=1, num_threads=4) 

Получив результаты статистической оценки, можно сделать выводы, различаются группы или нет.

Основной минус подхода: чем больше подгрупп — тем меньше мощность критерия, что увеличивает вероятность принять неверную гипотезу. Например, для десяти тестов и необходимо получить , чтобы сказать, что разница значимая. Чтобы нивелировать эти недостатки, можно выбрать метод Холма.

2. Метод Холма

Это нисходящая процедура последовательного изменения . На первом шаге алгоритма метода реальные сортируются по возрастанию:

затем корректируется исходно заданный -уровень:

после чего проверяется условие и делается заключение, верна ли основная гипотеза .

Точка останова алгоритма — момент i, когда принята первая основная гипотеза , при этом принимаются и все последующие .
Реализовать данный метод можно при помощи процедуры из библиотеки с параметром :

from bootstrapped import bootstrap as bs from bootstrapped import stats_functions as bs_st from scipy.stats import ttest_ind from statsmodels.sandbox.stats.multicomp import multipletests bs_a = bs.bootstrap(np.array(group_A), stat_func=bs_st.mean, num_iterations=10000, iteration_batch_size=300, return_distribution=True) bs_b = bs.bootstrap(np.array(group_B), stat_func=bs_st.mean, num_iterations=10000, iteration_batch_size=300, return_distribution=True) bs_c = bs.bootstrap(np.array(group_C), stat_func=bs_st.mean, num_iterations=10000, iteration_batch_size=300, return_distribution=True) stat_ab, p_ab = stats.ttest_ind(pd.DataFrame(bs_a), pd.DataFrame(bs_b)) stat_bc, p_bc = stats.ttest_ind(pd.DataFrame(bs_b), pd.DataFrame(bs_c)) stat_ac, p_ac = stats.ttest_ind(pd.DataFrame(bs_a), pd.DataFrame(bs_c)) print(sorted([p_ab, p_bc, p_ac])) print("FWER: " + str(multipletests(sorted([p_ab, p_bc, p_ac]), alpha=0.05, method='holm', is_sorted = True))) 

Контроль FDR

Контроль означает, что выполняется условие . При этом , т. е. вероятность получить ошибку первого рода при контроле снижается.

Метод Бенджамини — Хохберга

Эта восходящая процедура предполагает последовательное изменение , предварительно отсортированных по возрастанию:

Затем исходный -уровень корректируется по формуле:

затем, как и в методе Холма, проверяется условие и делается заключение, верна ли основная гипотеза и все последующие .

Метод Бенджамини — Хохберга, как и метод Холма, можно реализовать при помощи процедуры :

print("FDR: " + str(multipletests([p_ab, p_bc, p_ac], alpha=0.05, method='fdr_bh', is_sorted = False))) 

Заключение

В статье мы рассказали об основных методах оценки результатов множественных тестов и привели примеры программного кода, реализующего эти методы. Мы надеемся, что вы с пользой и интересом провели время и сможете применить описанные процедуры на практике. А если у вас возникли вопросы — мы с радостью ответим на них.

Источник