Метод конечных элементов питон

Introduction to FEM Analysis with Python¶

This tutorial aims to show using Python to pre-processing, solve, and post-processing of Finite Element Method analysis. It uses a finite element method library with a Python interface called GetFEM for preprocessing and solving. We will load vtk file by using meshio and visualize by matplotlib in pre-processing and post-processing. This tutorial was used in the PyConJP 2019 talk. You can watch the talk on YouTube below. This tutorial is based on the following official GetFEM page tutorial.

from IPython.display import YouTubeVideo YouTubeVideo("6JuB1GiDLQQ", start=512) 

Installation¶

GetFEM including its python interface can be installed from a terminal by executing aptitude update and aptitude install python3-getfem++.

sudo aptitude install python3-getfem++

The additional packages in requirements.txt are required for this tutorial. You do not need to build these environments because they are already configured in the Dockerfile.

The problem setting¶

The problem refers to “Poisson’s Equation on Unit Disk” published by Math Works’s homepage.

How to use GetEM¶

We take the following steps when using GetFEM to solve finite element problems. See this page for more information on using GetFEM.

• define a MesherObject
• define a Mesh
• define a MeshFem
• define a MeshIm
• define a Model and set it up
• solve Model object
• get value from Model object

Initialization¶

GetFEM can be imported as follows (numpy has also to be imported).

import getfem as gf import numpy as np 

Mesh generation¶

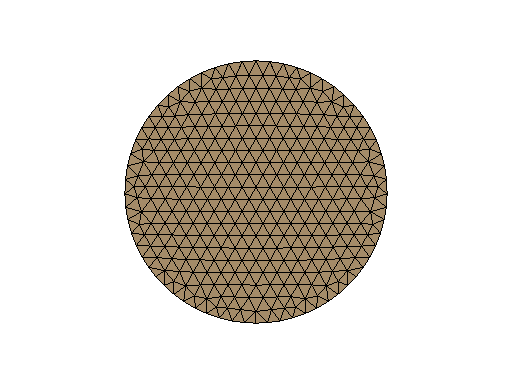
We use GetFEM’s MesherObject to create a mesh from the geometric information to be analyzed. This object represent a geometric object to be meshed by the experimental meshing procedure of GetFEM. We can represent a disk by specifying a radius, a 2D center, and using “ball” geometry.

center = [0.0, 0.0] radius = 1.0 mo = gf.MesherObject("ball", center, radius) 

We can make mesh object mesh by calling the experimental mesher of GetFEM on the geometry represented by mo . The approximate element diameter is given by h and the degree of the mesh is K ( \(K > 1\) for curved boundaries).

h = 0.1 K = 2 mesh = gf.Mesh("generate", mo, h, K) 

Boundary selection¶

To define a boundary condition, we set a boundary number on the outer circumference of the circle.

outer_faces = mesh.outer_faces() OUTER_BOUND = 1 mesh.set_region(OUTER_BOUND, outer_faces) 

Mesh draw¶

We visualize the created mesh to check its quality. We can output mesh objects, but matplotlib can only display triangles. Therefore, we make a Slice object with a slice operation of («none»,) , which does not cut the mesh. With a refinement of 1, this serves to convert the mesh to triangles.

We can export a slice to VTK file by using export_to_vtk method.

sl.export_to_vtk("sl.vtk", "ascii") 

We can render VTK files using Paraview or mayavi2. In order to display in the jupyter notebook this time, we read in meshio and draw in matplotlib.

import pyvista as pv from pyvirtualdisplay import Display display = Display(visible=0, size=(1280, 1024)) display.start() p = pv.Plotter() m = pv.read("sl.vtk") p.add_mesh(m, show_edges=True) pts = m.points p.show(window_size=[512, 384], cpos="xy") display.stop() 

Definition of finite element methods and integration method¶

We define the finite element and integration methods to use. We create a MeshFem that defines the degree of freedom of the mesh as rank 1 (scalar).

Next we set the finite element used. Classical finite element means a continuous Lagrange element. Setting elements_degree to 2 means that we will use quadratic (isoparametric) elements.

elements_degree = 2 mfu.set_classical_fem(elements_degree) 

The last thing to define is an integration method mim . There is no default integration method in GetFEM so it is mandatory to define an integration method. Of course, the order of the integration method has to be chosen sufficient to make a convenient integration of the selected finite element method. Here, the square of elements_degree is sufficient.

mim = gf.MeshIm(mesh, pow(elements_degree, 2)) 

Model definition¶

The model object in GetFEM gathers the variables of the models (the unknowns), the data and what are called the model bricks. The model bricks are some parts of the model (linear or nonlinear terms) applied on a single variable or linking several variables. A model brick is an object that is supposed to represent a part of a model. It aims to represent some integral terms in a weak formulation of a PDE model. They are used to make the assembly of the (tangent) linear system (see The model object for more details).

md = gf.Model("real") md.add_fem_variable("u", mfu) 

Poisson’s equation¶

To define Poisson’s equation, we have to define a Laplacian term and RHS source term. We can add the Laplacian term (which is called a brick in GetFEM) by using add_Laplacian_brick() .

md.add_Laplacian_brick(mim, "u") 

If you want to define constants in GetFEM, we use the add_fem_data() method.

F = 1.0 md.add_fem_data("F", mfu) 

We can set constant values with the set_variable() method. Here we pass a vector ( ndarray ) the size of the degrees of freedom.

md.set_variable("F", np.repeat(F, mfu.nbdof())) 

We define the term RHS with the add_source_term_brick() method, using the constant F just defined.

md.add_source_term_brick(mim, "u", "F") 

Finally, we set the Dirichlet condition at the boundary.

md.add_Dirichlet_condition_with_multipliers(mim, "u", elements_degree - 1, OUTER_BOUND) 

Model solve¶

Once the model is correctly defined, we can simply solve it by:

Export/visualization of the solution¶

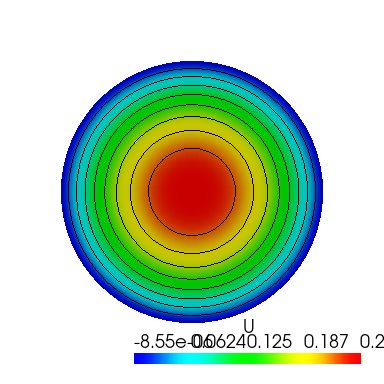
The finite element problem is now solved. We can get the solution \(u\) by using variable method.

We can output the computed u with the mesh of the Slice object.

sl.export_to_vtk("u.vtk", "ascii", mfu, U, "U") display = Display(visible=0, size=(1280, 1024)) display.start() p = pv.Plotter() m = pv.read("u.vtk") contours = m.contour() p.add_mesh(m, show_edges=False) p.add_mesh(contours, color="black", line_width=1) p.add_mesh(m.contour(8).extract_largest(), opacity=0.1) pts = m.points p.show(window_size=[384, 384], cpos="xy") display.stop() 

Exact solution¶

The exact solution to this problem is given by the following equation:

We can calculate the error for the L2 and H1 norms by using compute :

L2error = gf.compute(mfu, U - evalue, "L2 norm", mim) H1error = gf.compute(mfu, U - evalue, "H1 norm", mim) print("Error in L2 norm : ", L2error) print("Error in H1 norm : ", H1error) 

Error in L2 norm : 1.965329030567132e-06 Error in H1 norm : 0.00010936971229957788

As you can see, the size of the error is within the acceptable range.

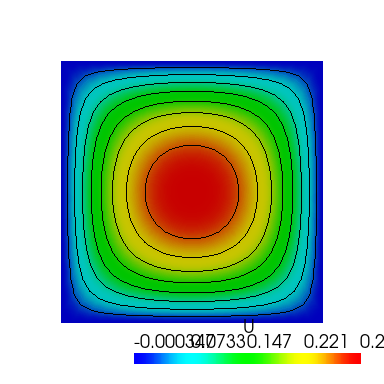
Quadrangular shape case¶

Even if the shape of the region is different, GetFEM can obtain a finite element solution by rewriting the program a little. In the case of a quadrangular shape it may be calculated for:.

# Mesh generation mo = gf.MesherObject("rectangle", [-1.0, -1.0], [1.0, 1.0]) h = 0.1 K = 2 mesh = gf.Mesh("generate", mo, h, K) # Boundary selection outer_faces = mesh.outer_faces() OUTER_BOUND = 1 mesh.set_region(OUTER_BOUND, outer_faces) sl = gf.Slice(("none",), mesh, 1) sl.export_to_vtk("sl.vtk", "ascii") # Mesh draw display = Display(visible=0, size=(1280, 1024)) display.start() p = pv.Plotter() m = pv.read("sl.vtk") p.add_mesh(m, show_edges=True) pts = m.points p.show(window_size=[512, 384], cpos="xy") display.stop() 

# Definition of finite element methods and integration method mfu = gf.MeshFem(mesh, 1) elements_degree = 2 mfu.set_classical_fem(elements_degree) mim = gf.MeshIm(mesh, pow(elements_degree, 2)) # Model definition md = gf.Model("real") md.add_fem_variable("u", mfu) # Poisson’s equation md.add_Laplacian_brick(mim, "u") F = 1.0 md.add_fem_data("F", mfu) md.set_variable("F", np.repeat(F, mfu.nbdof())) md.add_source_term_brick(mim, "u", "F") md.add_Dirichlet_condition_with_multipliers(mim, "u", elements_degree - 1, OUTER_BOUND) # Model solve md.solve() # Export/visualization of the solution U = md.variable("u") sl.export_to_vtk("u.vtk", "ascii", mfu, U, "U") display = Display(visible=0, size=(1280, 1024)) display.start() p = pv.Plotter() m = pv.read("u.vtk") contours = m.contour() p.add_mesh(m, show_edges=False) p.add_mesh(contours, color="black", line_width=1) p.add_mesh(m.contour(8).extract_largest(), opacity=0.1) pts = m.points p.show(window_size=[384, 384], cpos="xy") display.stop() 

© Copyright 2020, Tetsuo Koyama Revision d8b11ffb .

Versions latest stable Downloads html On Read the Docs Project Home Builds Free document hosting provided by Read the Docs.

Источник

Documentation of scikit-fem¶

scikit-fem is a pure Python 3.7+ library for performing finite element assembly. Its main purpose is the transformation of bilinear forms into sparse matrices and linear forms into vectors. The library supports triangular, quadrilateral, tetrahedral and hexahedral meshes as well as one-dimensional problems.

Installing the library is as simple as running

Remove [all] to not install the optional dependencies meshio and matplotlib .

Table of contents¶

• Documentation of scikit-fem
• Getting started
  • Step 1: Clarify the problem
  • Step 2: Express the forms as code
  • Step 3: Create a mesh
  • Step 4: Define a basis
  • Step 5: Assemble the linear system
  • Step 6: Find boundary DOFs
  • Step 7: Eliminate boundary DOFs and solve
  • Step 8: Calculate error
  • Finding degrees-of-freedom
  • Performing projections
  • Discrete functions in forms
  • Assembling jump terms
  • Anatomy of forms
  • Indexing of the degrees-of-freedom
  • Poisson equation
    • Example 1: Poisson equation with unit load
    • Example 7: Discontinuous Galerkin method
    • Example 12: Postprocessing
    • Example 13: Laplace with mixed boundary conditions
    • Example 14: Laplace with inhomogeneous boundary conditions
    • Example 15: One-dimensional Poisson equation
    • Example 9: Three-dimensional Poisson equation
    • Example 22: Adaptive Poisson equation
    • Example 37: Mixed Poisson equation
    • Example 38: Point source
    • Example 40: Hybridizable discontinuous Galerkin method
    • Example 41: Mixed meshes
    • Example 2: Kirchhoff plate bending problem
    • Example 3: Linear elastic eigenvalue problem
    • Example 4: Linearized contact problem
    • Example 8: Argyris basis functions
    • Example 11: Three-dimensional linear elasticity
    • Example 21: Structural vibration
    • Example 34: Euler-Bernoulli beam
    • Example 36: Nearly incompressible hyperelasticity
    • Example 43: Hyperelasticity
    • Example 18: Stokes equations
    • Example 20: Creeping flow via stream-function
    • Example 24: Stokes flow with inhomogeneous boundary conditions
    • Example 29: Linear hydrodynamic stability
    • Example 30: Krylov-Uzawa method for the Stokes equation
    • Example 32: Block diagonally preconditioned Stokes solver
    • Example 42: Periodic meshes
    • Example 17: Insulated wire
    • Example 19: Heat equation
    • Example 25: Forced convection
    • Example 26: Restricting problem to a subdomain
    • Example 28: Conjugate heat transfer
    • Example 39: One-dimensional heat equation
    • Example 10: Nonlinear minimal surface problem
    • Example 16: Legendre’s equation
    • Example 31: Curved elements
    • Example 33: H(curl) conforming model problem
    • Example 35: Characteristic impedance and velocity factor
    • Example 44: Wave equation
    • Module: skfem.mesh
      • Abstract class: Mesh
        • Class: MeshTri
        • Class: MeshQuad
        • Class: MeshTet
        • Class: MeshHex
        • Class: MeshLine
        • Abstract class: AbstractBasis
          • Class: CellBasis
          • Class: FacetBasis
          • Class: InteriorFacetBasis
          • Class: BilinearForm
          • Class: LinearForm
          • Class: Functional
          • Function: solve
          • Function: condense
          • Function: enforce

          Источник