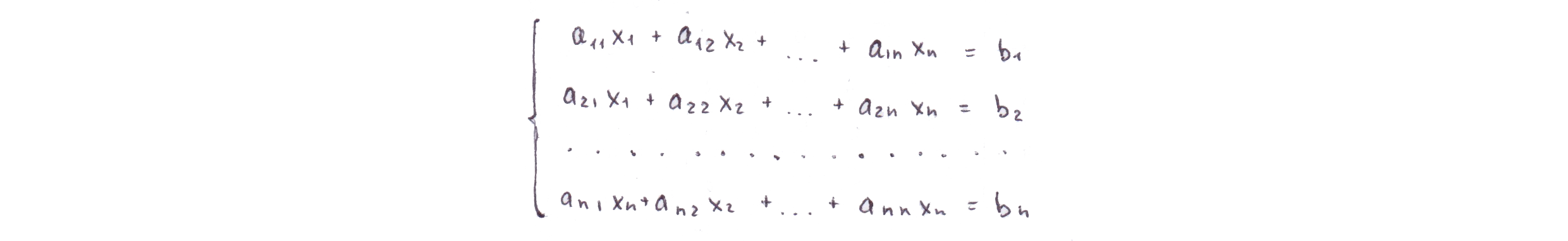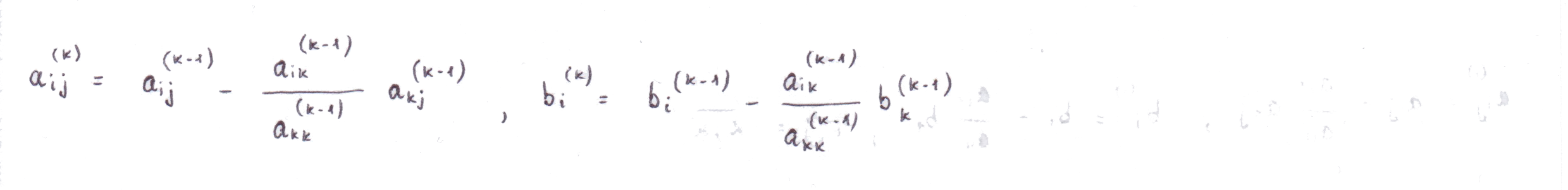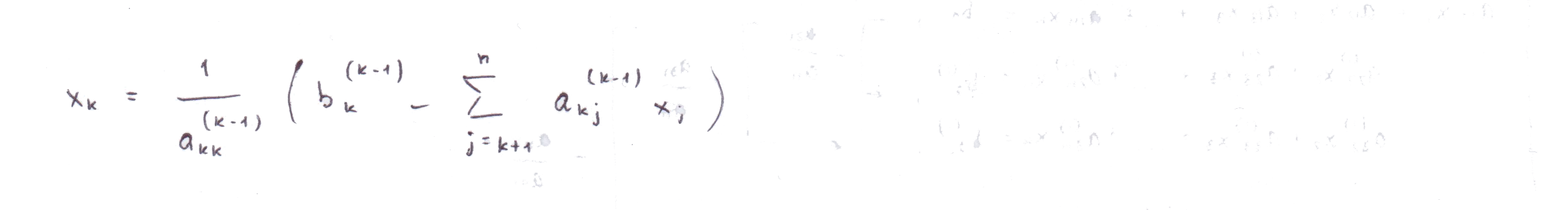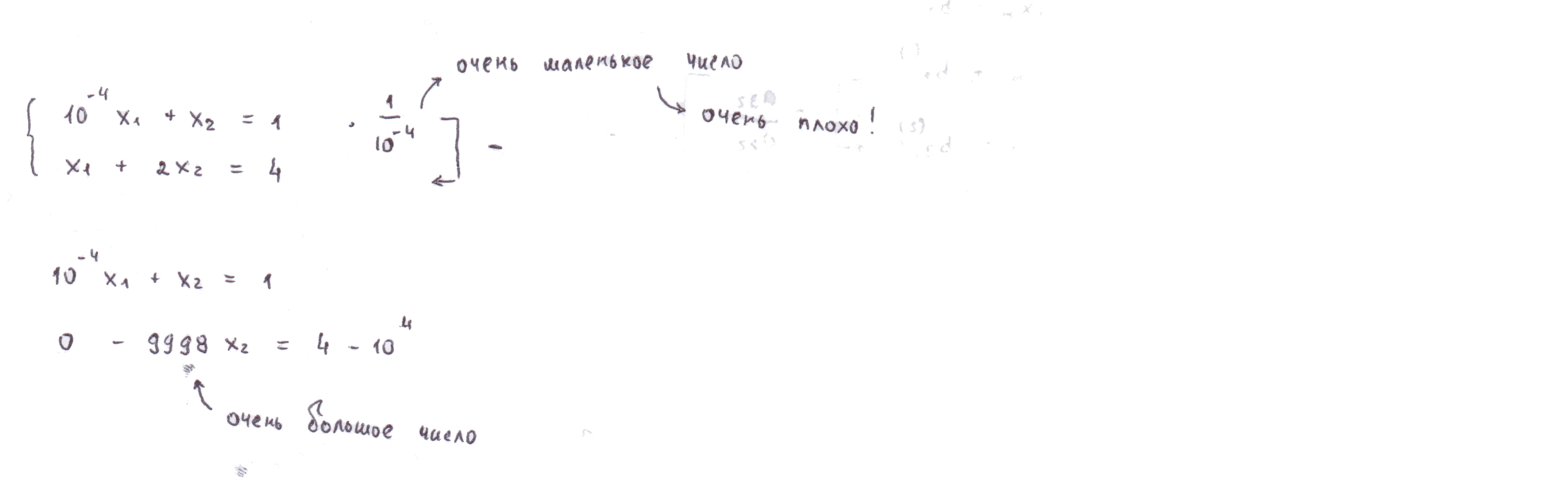Метод гаусса python код программы

МЕТОД ГАУССА PYTHON

Метод Гаусса (или метод исключения Гаусса) — один из основных методов решения систем линейных уравнений. В Python этот метод можно реализовать с помощью матричных операций. Для этого можно воспользоваться библиотекой NumPy:

matrix = np.array([[2, 1, -1], [4, -1, 2], [-1, 2, 5]])
target = np.array([1, 2, 3])

result = np.linalg.solve(matrix, target)

В данном примере мы создаем матрицу коэффициентов и столбец свободных членов, а затем применяем функцию solve из библиотеки NumPy для решения системы линейных уравнений. Результатом работы функции является массив, содержащий значения неизвестных.

Однако, следует помнить, что метод Гаусса имеет некоторые ограничения, так как некоторые системы линейных уравнений могут быть плохо обусловлены и метод может давать неточный результат. Поэтому перед применением этого метода следует оценивать обусловленность системы и, при необходимости, использовать другие методы решения.

Метод Ньютона — Лучший момент из фильма Двадцать одно 21

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)

Математика без Ху%!ни. Метод Гаусса.

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэ

4 совета как ЛУЧШЕ писать циклы For на Python

Задача из Собеседования в Амазон: Поиск Знаменитости. Метод двух указателей

Решение систем линейных матричных уравнений через формулы Крамера в Python

• Параметрический полиморфизм python
• Курсы hexlet python скачать
• Api мой склад python
• Numpy изменить тип массива
• Константы в python
• Код игры на python марио
• Python среднее геометрическое
• Etl на python
• Линейный алгоритм python
• Как передать переменную из одного класса в другой python
• Python бинарный поиск
• Мемы про python
• Отступы в python

Источник

Решение системы уравнений методом Гаусса на Python

Решение системы уравнений методом Гаусса является одним из фундаментальных заданий линейной алгебры. Этот метод основан на элементарных преобразованиях строк матрицы системы уравнений и позволяет свести ее к эквивалентной треугольной форме. В этой статье мы покажем Вам, как реализовать алгоритм метода Гаусса на Python.

Алгоритм метода Гаусса

Метод Гаусса заключается в последовательном применении трех типов элементарных преобразований над строками расширенной матрицы системы уравнений, где в последнем столбце записаны свободные члены уравнений.

Эти преобразования включают в себя:

1. Перестановка двух строк матрицы местами;
2. Умножение строки на ненулевое число;
3. Прибавление к одной строке другой строке, умноженной на число.

Цель алгоритма Гаусса – привести матрицу системы к ступенчатому виду, то есть к матрице, в которой первый ненулевой элемент каждой строки находится правее первого ненулевого элемента предыдущей строки. Затем полученную матрицу можно привести к диагональному виду методом обратных ходов.

Когда матрица системы находится в диагональном виде, можно легко найти решение системы линейных уравнений, обратившись к коэффициентам при неизвестных, записанным на главной диагонали матрицы.

Решение СЛАУ методом Гаусса на Python

• Для решения СЛАУ методом Гаусса мы будем использовать библиотеку numpy, которая позволит сделать код чище и читаемее за счёт вынесения некоторой логики на уровень абстракции.

• Далее мы зададим начальные значения для матрицы системы уравнений и столбца свободных членов. Далее, мы вынесем это в функцию с принимаемыми аргументами.

A = np.array([[2.7, 3.3, 1.3], [3.5, -1.7, 2.8], [4.1, 5.8, -1.7]]) B = np.array([2.1, 1.7, 0.8])

• Согласно формуле метода Гаусса, по нему необходимо пройтись циклом. Длина цикла будет равна длине массива свободных членов (B).

• В цикле в первую очередь нам нужно найти максимальный элемент в каждом столбце. Т.е. при каждой итерации цикла мы будем искать в i-том столбце.

 maxEl = abs(A[i][i]) maxRow = i for k in range(i + 1, n): if abs(A[k][i]) > maxEl: maxEl = abs(A[k][i]) maxRow = k

 for k in range(i, n): tmp = A[maxRow][k] A[maxRow][k] = A[i][k] A[i][k] = tmp tmp = B[maxRow] B[maxRow] = B[i] B[i] = tmp

• После того, как мы поставили строки в нужном порядке, нам необходимо привести систему линейных уравнений к треугольному виду. Т.е., сделать так, чтобы все нули образовывали треугольник, а значения были вторым треугольником.

 for k in range(i + 1, n): c = -A[k][i] / A[i][i] for j in range(i, n): if i == j: A[k][j] = 0 else: A[k][j] += c * A[i][j] B[k] += c * B[i]

• Далее мы делаем обратный ход, который является последней операцией над СЛАУ для решения её методом Гаусса.

x = np.zeros(n) for i in range(n - 1, -1, -1): x[i] = B[i] for j in range(i + 1, n): x[i] -= A[i][j] * x[j] x[i] /= A[i][i]

Полный код решения СЛАУ методом Гаусса на Python

import numpy as np # Определяем матрицу системы уравнений A = np.array([[2.7, 3.3, 1.3], [3.5, -1.7, 2.8], [4.1, 5.8, -1.7]]) # Определяем столбец свободных членов B = np.array([2.1, 1.7, 0.8]) # Прямой ход метода Гаусса n = len(B) for i in range(n): # Поиск максимального элемента в столбце i maxEl = abs(A[i][i]) maxRow = i for k in range(i + 1, n): if abs(A[k][i]) > maxEl: maxEl = abs(A[k][i]) maxRow = k # Обмен строками for k in range(i, n): tmp = A[maxRow][k] A[maxRow][k] = A[i][k] A[i][k] = tmp tmp = B[maxRow] B[maxRow] = B[i] B[i] = tmp # Приведение к верхнетреугольному виду for k in range(i + 1, n): c = -A[k][i] / A[i][i] for j in range(i, n): if i == j: A[k][j] = 0 else: A[k][j] += c * A[i][j] B[k] += c * B[i] # Обратный ход метода Гаусса x = np.zeros(n) for i in range(n - 1, -1, -1): x[i] = B[i] for j in range(i + 1, n): x[i] -= A[i][j] * x[j] x[i] /= A[i][i] # Вывод результата print("Result:") print(x)

Результат выполнения кода:

Выделим код в отдельную функцию

Для того, чтобы алгоритм был более универсальным и вы могли его скопировать к себе в проект, я выделю функцию, которая будет принимать на вход все нужные аргументы и выводить конечный результат. Всё, что вам останется, это скопировать функцию и передать ей правильные аргументы. Итак, готовый код:

import numpy as np def gauss(A, B): # Прямой ход метода Гаусса n = len(B) for i in range(n): # Поиск максимального элемента в столбце i maxEl = abs(A[i][i]) maxRow = i for k in range(i + 1, n): if abs(A[k][i]) > maxEl: maxEl = abs(A[k][i]) maxRow = k # Обмен строками for k in range(i, n): tmp = A[maxRow][k] A[maxRow][k] = A[i][k] A[i][k] = tmp tmp = B[maxRow] B[maxRow] = B[i] B[i] = tmp # Приведение к верхнетреугольному виду for k in range(i + 1, n): c = -A[k][i] / A[i][i] for j in range(i, n): if i == j: A[k][j] = 0 else: A[k][j] += c * A[i][j] B[k] += c * B[i] # Обратный ход метода Гаусса x = np.zeros(n) for i in range(n - 1, -1, -1): x[i] = B[i] for j in range(i + 1, n): x[i] -= A[i][j] * x[j] x[i] /= A[i][i] return x # Определяем матрицу системы уравнений A = np.array([[2.7, 3.3, 1.3], [3.5, -1.7, 2.8], [4.1, 5.8, -1.7]]) # Определяем столбец свободных членов B = np.array([2.1, 1.7, 0.8]) x = gauss(A, B) # Вывод результата print("Result:") print(x)

Источник

Численные методы на Python

Метод Гаусса является наиболее известным методом решения систем линейных уравнений. Суть метода заключается в последовательном исключении неизвестных. Ниже выводится совокупность формул, позволяющих в итоге получить значения неизвестных. Метод Гаусса состоит из двух этапов — прямого хода и обратного хода.

Рассмотрим систему линейных уравнений вида

Прямой ход

Задача прямого хода заключается в приведении системы к треугольному виду. Первый шаг — исключим из второго, третьего, . n-го уравнений. Второй шаг — исключим из третьего, четвертого, . n-го уравнений и т.д. Результатом первого шага будет система коэффициенты с верхним индексом 1 (верхний индекс показывает номер шага) подсчитываются по формулам Результатом второго шага будет система Заметим, что коэффициенты для второго шага вычисляются по формулам Продолжая процесс на (n-1) шаге система приобретает треугольный вид Коэффициенты этой системы могут быть получены с помощью формул общего вида:

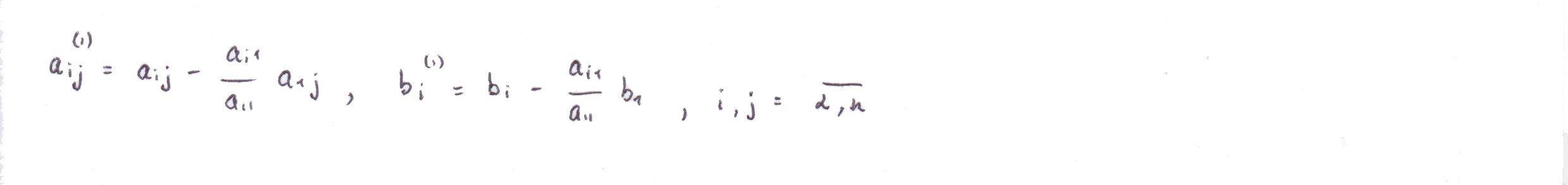
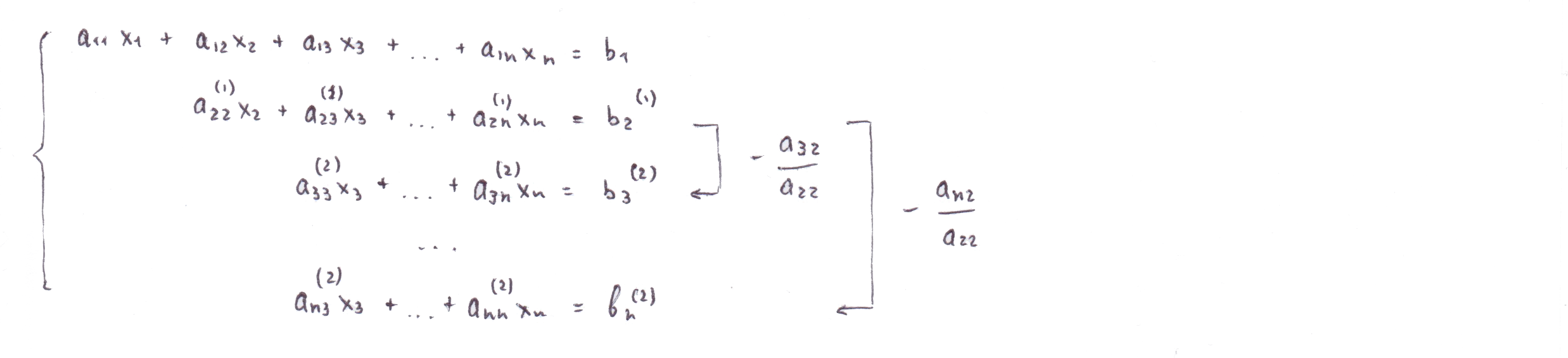
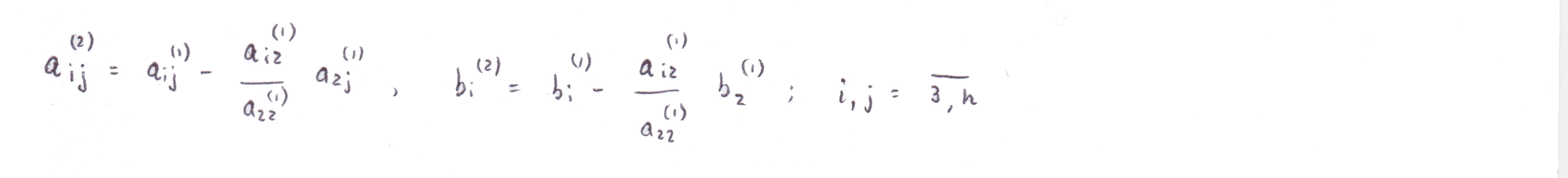
Обратный ход

Заключается в вычислении неизвестных, начиная с последнего и двигаясь вверх. Для нахождения вычислим простую дробь Для нахождения Для первых неизвестных формулы принимают следующий вид Исходя из вышеприведенных уравнений возможно сфомулировать общую формулу обратного хода

Постолбцовый выбор главных элементов

Так как реальные машинные вычисления производятся с усеченными числами, неизбежны ошибки округления. Если на каком-то этапе знаменатели дробей окажуться слишком маленькими, выполнение алгоритма может привести к неверным результатам. Рассмотрим пример Вычтем из второй строчки первую, умноженную на Подставляя в первую строчку Подставляя во вторую строчку найденные и имеем Решим ту же систему, поменяв местами строчки в исходной системе Подставляя полученные значения в систему, получаем результат, более приблеженный к реальности, чем результат из предыдущего решения. Чтобы уменьшить влияние ошибок округления и исключить деление на нуль на каждом этапе прямого хода, уравнения системы решено переставлять так, чтобы деление проводилось на наибольший по модулю в данном столбце элемент (что было сделано во втором варианте решения). Это делается с целью избежания ситуаций, когда близко к нулю. Если это так, то результатом деления на оказатся большое число с большой абсолютной погрешностью. Числа, на которые производится деление в методе Гаусса, называются ведущими или главными элементами. Таким образом, в начале каждого этапа прямого хода решения системы следует добавить логику перестановки строк для выполнения приведенного условия.

Реализация

from matrix_api import * def bubble_max_row(m, col): """Replace m[col] row with the one of the underlying rows with the modulo greatest first element. :param m: matrix (list of lists) :param col: index of the column/row from which underlying search will be launched :return: None. Function changes the matrix structure. """ max_element = m[col][col] max_row = col for i in range(col + 1, len(m)): if abs(m[i][col]) > abs(max_element): max_element = m[i][col] max_row = i if max_row != col: m[col], m[max_row] = m[max_row], m[col] def solve_gauss(m): """Solve linear equations system with gaussian method. :param m: matrix (list of lists) :return: None """ n = len(m) # forward trace for k in range(n - 1): bubble_max_row(m, k) for i in range(k + 1, n): div = m[i][k] / m[k][k] m[i][-1] -= div * m[k][-1] for j in range(k, n): m[i][j] -= div * m[k][j] # check modified system for nonsingularity if is_singular(m): print('The system has infinite number of answers. ') return # backward trace x = [0 for i in range(n)] for k in range(n - 1, -1, -1): x[k] = (m[k][-1] - sum([m[k][j] * x[j] for j in range(k + 1, n)])) / m[k][k] # Display results display_results(x) def is_singular(m): """Check matrix for nonsingularity. :param m: matrix (list of lists) :return: True if system is nonsingular """ for i in range(len(m)): if not m[i][i]: return True return False m = read_matrix('matrix10x10.txt') solve_gauss(m) 

Векторная реализация

Рассматривается реализация с использованием векотрых операций при помощи библиотеки numpy

import numpy as np from matrix_np_api import * def bubble_max_row(m, k): """Replace m[col] row with the one of the underlying rows with the modulo greatest first element. :param m: numpy matrix :param k: number of the step in forward trace :return: None. Function changes the matrix structure. """ ind = k + np.argmax(np.abs(m[k:, k])) if ind != k: m[k, :], m[ind, :] = np.copy(m[ind, :]), np.copy(m[k, :]) def solve_gauss(m): """Solve linear equations system with gaussian method. :param m: numpy matrix :return: None """ n = m.shape[0] # forward trace for k in range(n - 1): bubble_max_row(m, k) for i in range(k + 1, n): # modify row frac = m[i, k] / m[k, k] m[i, :] -= m[k, :] * frac # check modified system for nonsingularity if is_singular(m): print('The system has infinite number of answers. ') return # backward trace x = np.matrix([0.0 for i in range(n)]).T for k in range(n - 1, -1, -1): x[k, 0] = (m[k, -1] - m[k, k:n] * x[k:n, 0]) / m[k, k] # Display results display_results(x) def is_singular(m): """Check matrix for nonsingularity. :param m: matrix (list of lists) :return: True if system is nonsingular """ return np.any(np.diag(m) == 0) m = read_matrix('matrix10x10.txt') solve_gauss(m) 

Источник