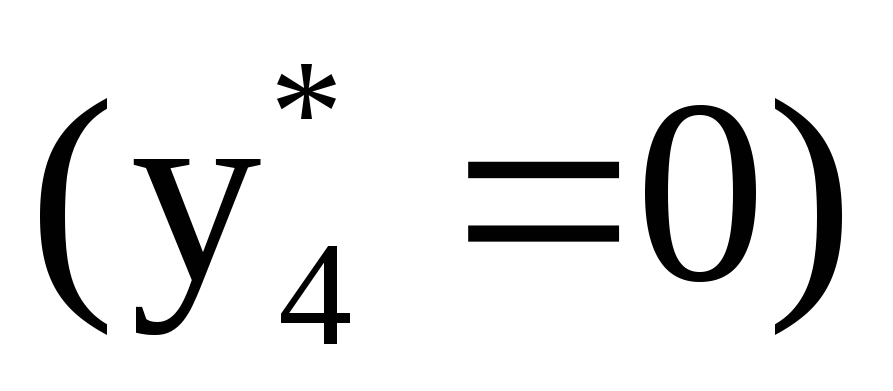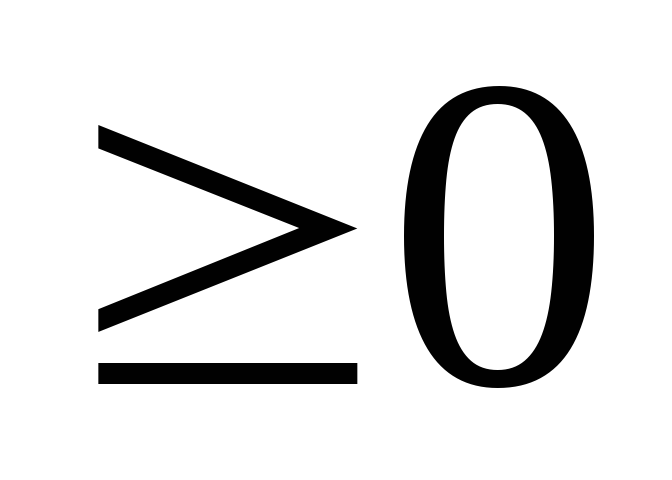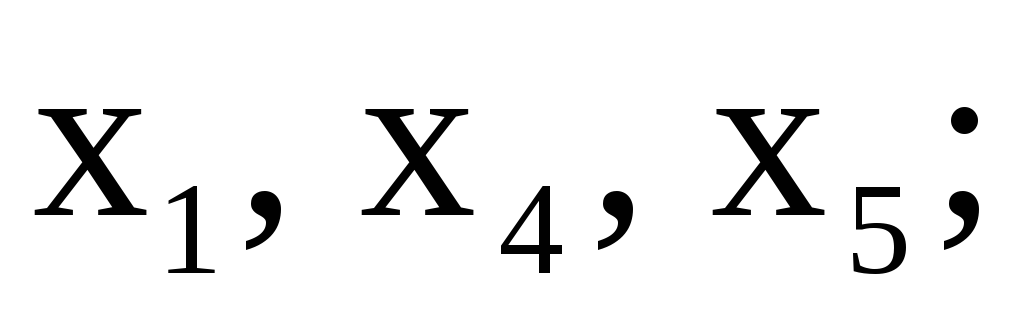Двойственный симплексный метод
Двойственный симплексный метод основан на теории двойственности (см. решение двойственной задачи) и используется для решения задач линейного программирования, свободные члены которых bi могут принимать любые значения, а система ограничений задана неравенствами смысла «≤», «≥» или равенством «=».
Инструкция для решения задач двойственным симплекс-методом. Выберите количество переменных и количество строк (количество ограничений), нажмите Далее . Полученное решение сохраняется в файле Word . При этом ограничения типа xi≥0 не учитывайте.
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.
| Объем товара Х (в партиях) | Доход G(X) | ||
| 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 |
| 1 | 28 | 30 | 32 |
| 2 | 41 | 42 | 45 |
| 3 | 50 | 55 | 48 |
| 4 | 62 | 64 | 60 |
| 5 | 76 | 76 | 72 |
- Составление псевдоплана. Систему ограничений исходной задачи приводят к системе неравенств смысла «≤».
- Проверка плана на оптимальность. Если в полученном опорном плане не выполняется условие оптимальности, то задача решается симплексным методом.
- Выбор ведущих строки и столбца. Среди отрицательных значений базисных переменных выбираются наибольшие по абсолютной величине. Строка, соответствующая этому значению, является ведущей.
- Расчет нового опорного плана. Новый план получается в результате пересчета симплексной таблицы методом Жордана-Гаусса. Далее переход к этапу 2.
Алгоритм двойственного симплекс-метода
Пример решения Р-методом
Условие задачи. Предприятию необходимо выпустить по плану продукции А1– 500 единиц, А2– 300 единиц, А3– 450 единиц. Каждый вид изделия может производиться на двух машинах.
Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальны? Дана матрица затрат и ресурс времени каждой машины. Записать модель исследуемой операции в форме, допускающей использование P – метода.
| Матрица затрат времени на производство видов продукции g – го вида A=(aig) | ||||
| Машины | Виды продукции | Ресурс времени машин | ||
| А1 | А2 | А3 | ||
| 1 | 2 | 3 | 3 | 1500 |
| 2 | 5 | 4 | 1 | 1000 |
| План выпуска продукции | 500 | 300 | 450 | |
Составим математическую модель задачи.
2x11+ 3x12+3x13≤ 1500
5x21+ 4x22+x23≤ 1000
x11+ x21≥ 500
x12+ x22≥ 300
x13+ x23≥ 450
Целевая функция:
2x11+ 3x12+3x13+ 5x21+ 4x22+x23→ min
Запишем в виде, решаемом Р-методом.
2x11+ 3x12+3x13≤ 1500
5x21+ 4x22+x23≤ 1000
-x11 -x21≤ -500
-x12-x22≤ -300
-x13-x23≤ -450
Определим минимальное значение целевой функции F(X) = 2x1+3x2+3x3+5x4+4x5+x6при следующих условиях-ограничений.
2x1+3x2+3x3≤1500
5x4+4x5+x6≤1000
-x1-x4≤-500
-x2-x5≤-300
-x3-x6≤-450
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2x1+ 3x2+ 3x3+ 0x4+ 0x5+ 0x6+ 1x7+ 0x8+ 0x9+ 0x10+ 0x11= 1500
0x1+ 0x2+ 0x3+ 5x4+ 4x5+ 1x6+ 0x7+ 1x8+ 0x9+ 0x10+ 0x11= 1000
-1x1+ 0x2+ 0x3-1x4+ 0x5+ 0x6+ 0x7+ 0x8+ 1x9+ 0x10+ 0x11= -500
0x1-1x2+ 0x3+ 0x4-1x5+ 0x6+ 0x7+ 0x8+ 0x9+ 1x10+ 0x11= -300
0x1+ 0x2-1x3+ 0x4+ 0x5-1x6+ 0x7+ 0x8+ 0x9+ 0x10+ 1x11= -450
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| 2 | 3 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 5 | 4 | 1 | 0 | 1 | 0 | 0 | 0 |
| -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных:
x7, x8, x9, x10, x11,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,0,0,0,1500,1000,-500,-300,-450)
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 0 | x7 | 1500 | 2 | 3 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| x8 | 1000 | 0 | 0 | 0 | 5 | 4 | 1 | 0 | 1 | 0 | 0 | 0 | |
| x9 | -500 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| x10 | -300 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | 0 | |
| x11 | -450 | 0 | 0 | -1 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 1 | |
| Индексная строка | F(X0) | 0 | -2 | -3 | -3 | -5 | -4 | -1 | 0 | 0 | 0 | 0 | 0 |
| θ | 2 | 5 |
Посмотреть все итерации Оптимальный план можно записать так: x5 = 133.33, x8 = 16.67, x1 = 500, x2 = 166.67, x6 = 450
F(X) = 2*500 + 3*166.67 + 4*133.33 + 1*450 = 2483.33 Пример №1 . Предприятию необходимо выпустить по плану продукции, не менее, чем: А 1 — 500 единиц, А2 – 300 единиц, А 3 – 450 единиц. Каждый вид изделия может производиться на двух машинах. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Ресурс времени каждой машины приведен справа от таблицы. Записать модель исследуемой операции в форме, допускающей использование Р-метода. Решить задачу Р-методом. Пример №2 . Из 4 видов кормов необходимо составить рацион, в состав которого должно входить не менее в1 ед. вещества А, в 2 ед. вещества В и в 3 ед. вещества С. Количество единиц вещества, содержащегося в 1 кг корма каждого вида, указано в соответствующей таблице. В ней же приведена цена 1 кг корма каждого вида.
Составить рацион, содержащий не менее нужного количества указанных питательных веществ и имеющий минимальную стоимость.
Алгоритм двойственного симплекс метода
Шаг 2. Просмотреть столбец свободных членов текущей таблицы (кроме элемента в строке целевой функции).
а) Если в столбце свободных членов нет отрицательных элементов (все ), то текущий базисный план – оптимальный.
б) Если в столбце свободных членов отрицательные элементы, выбирать среди них наибольший по модулю и объявить соответствующую строку разрешающей.
Шаг 3. Просмотреть разрешающую строку текущей таблицы (кроме элемента в столбце свободных членов)
а) Если в разрешающей строке нет отрицательных элементов (все ), то задача не имеет допустимых планов, и, следовательно, не разрешима.
б) Если в разрешающей строке есть отрицательные элементы, для всех содержащих эти элементы столбцов вычислить и записать в строку отношения коэффициентов строки целевой функции к соответствующим (отрицательным) элементам разрешающей строки –двойственные симплексные отношения. Столбец с минимальным по модулю двойственным симплексным отношением объявить разрешающим, элемент на пересечении разрешающего столбца с разрешающей строкой объявить разрешающим.
Шаг 4. Выполнить симплексное преобразование текущей таблицы с разрешающим элементом, выбранным на шаге 3б); объявить полученную таблицу и соответствующий базисный план текущими.
Шаг 5. Перейти к шагу 2.
Двойственный симплекс-метод «выгодно» применять, когда легко находится какая-нибудь симплексная таблица, удовлетворяющая условию оптимальности ( т. е. допустимая таблица двойственной задачи).
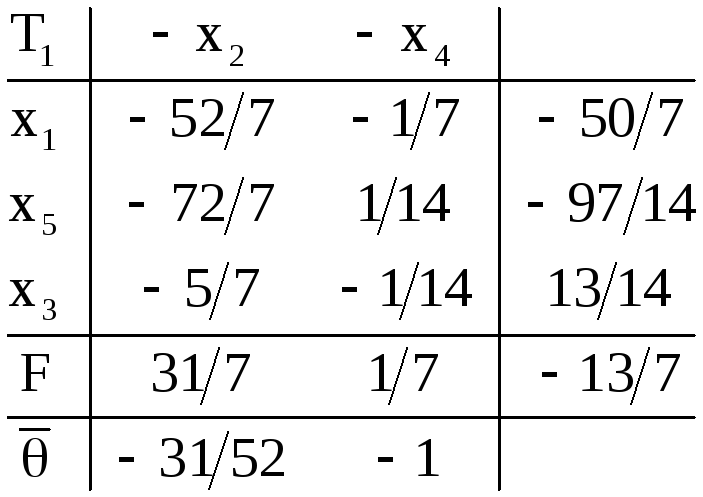
Пример 18. Решить задачу ЛП
Решение. Здесь нет «очевидных» начальных базисных переменных для применения обычного симплекс-метода; чтобы найти начальную таблицу, пришлось бы предварительно решить вспомогательную задачу (см. п. 5). Заметим, что выражение F содержит только две переменные, 
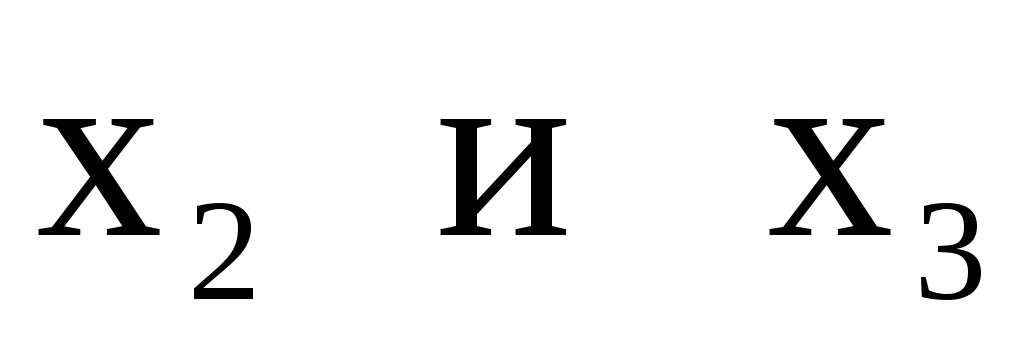










В 




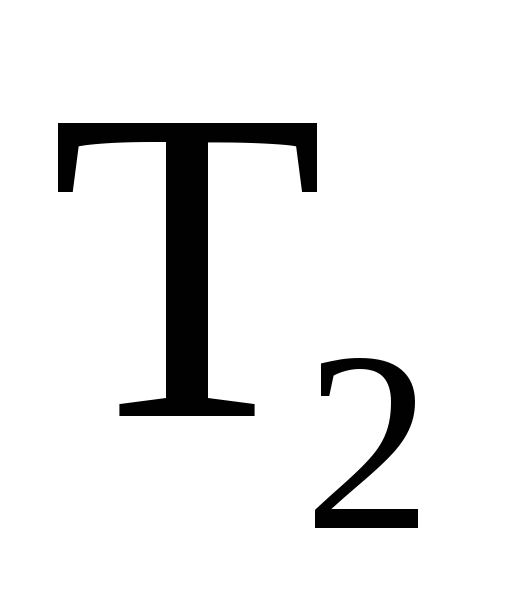

Типичными примерами задач с очевидной начальной таблицей для двойствен ного симплекс-метода являются задача о диете (7) – (9) и задача о раскрое.
Пример 19. Листы материала размером 

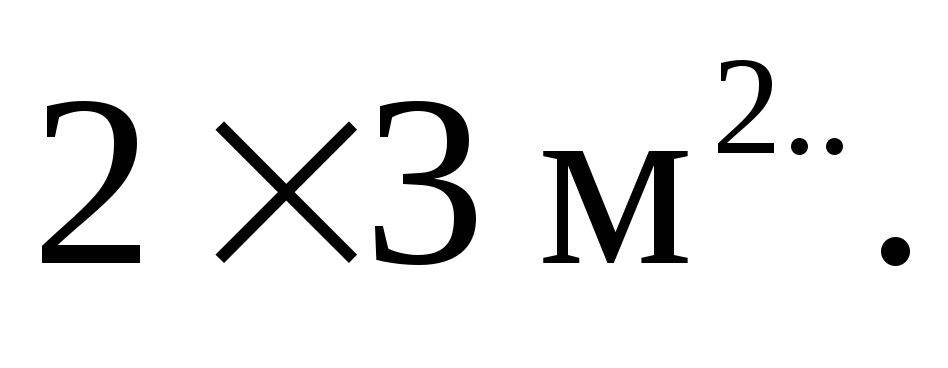
Решение. В условиях задачи способ раскроя листа полностью определяется парой чисел 



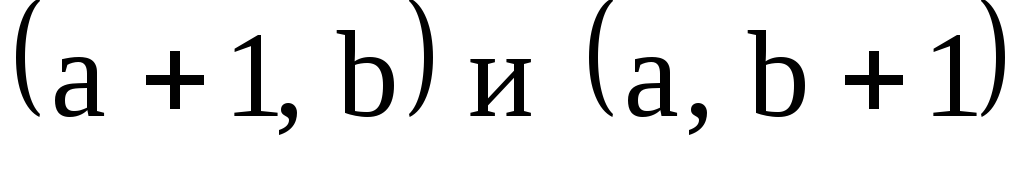
Пусть 





Каноническая форма этой задачи имеет вид
Таблица 

число заготовок можно получить из 275 листов, раскроив 250 из них первым способом и 25 – вторым способом.
В заключение выясним экономический смысл оптимальных значений переменных двойственной задачи (31) – (33) в случае, когда прямая задача (14) – (17) рассматривается как модель задачи о ресурсах. Напомним, что в этом случае правые части 



В примере 21 следующего п.7 будет показано, что 


Из последнего равенства видно, что при 





Используя понятие дефицитности и теневых цен ресурсов, можно дать экономическое истолкование постановке двойственной задачи (31) – (33) и утверждениям теорем двойственности. В частности, вторая группа уравнений теоремы 2 означает, что дефицитные ресурсы 



Пример 20. Построить модель задачи о ценности ресурсов для задачи о ресурсах из примера 11. Найти ценности и определить статус (дефицитные, недефицитные) ресурсов, указать самый ценный ресурс.
Решение. Моделью задачи о ценности ресурсов является задача ЛП, двойственная к модели самой задачи о ресурсах. Условие этой задачи записано в примере15. Ценности ресурсов, т. е. компоненты оптимального плана двой-
ственной задачи, можно найти непосредственно по заключительной таблице