Prim’s Algorithm in Java
1. Create a priority queue Q of NodeCost objects ( node, cost ). 2. Push [ S, 0 ] ( node, cost ) in the priority queue Q i.e Cost of reaching the node S from source node S is zero. 3. While ( ! Q.empty() ) 4. Object = Q.top(); Q.pop() 5. Node N = Object.Node and Cost C = Object.Cost 6. If the node N is not present in the spanning tree 7. Add node N to the spanning tree. 8. Cost of the spanning tree += Cost C 9. For all the nodes adjacent to node N that are not in the spanning tree. 10. Push object ( adjacent node, cost ) into the Q
Example of finding the minimum spanning tree using Prim’s algorithm
Time complexity of Prim’s algorithm : O((E+V)log(V))
- The time required to fetch the least expensive pair(cost, node) from the priority_queue is log V. This happens for every node V in the queue. Thus the time complexity for this operation is V(log(V)).
- The for loop only iterates through all the outgoing edges of every node. Since the graph is undirected, the total number of edges is 2E. Also, for every edge the pair (cost, node) is pushed into the priority-queue which takes log(V) time. Thus the maximum number of push operations can happen only 2E times giving the time-complexity of 2E(log(V)).
- From Operation 1. and Operation 2. the overall time complexity is O(V(log(V))) + O(2E(log(V))) = O((E+V)log(V)).
Java Prim’s minimum spanning tree algorithm
import java.util.ArrayList; import java.util.Arrays; import java.util.List; import java.util.Collections; import java.util.PriorityQueue; import java.util.Comparator; class NodeCost int node; // Adjacent node int cost; // Costance/cost to adjacent node NodeCost (int node, int cost) this.node = node; this.cost = cost; > > class Prims int Find_MST(int source_node, ListListNodeCost>> graph) // Comparator lambda function that enables the priority queue to store the nodes // based on the cost in the ascending order. ComparatorNodeCost> NodeCostComparator = (obj1, obj2) -> return obj1.cost - obj2.cost; >; // Priority queue stores the object node-cost into the queue with // the smallest cost node at the top. PriorityQueueNodeCost> pq = new PriorityQueue<>(NodeCostComparator); // The cost of the source node to itself is 0 pq.add(new NodeCost(source_node, 0)); boolean added[] = new boolean[graph.size()]; Arrays.fill(added, false); int mst_cost = 0; while (!pq.isEmpty()) // Select the item with minimum cost NodeCost item = pq.peek(); pq.remove(); int node = item.node; int cost = item.cost; // If the node is node not yet added to the minimum spanning tree, add it and increment the cost. if ( !added[node] ) mst_cost += cost; added[node] = true; // Iterate through all the nodes adjacent to the node taken out of priority queue. // Push only those nodes (node, cost) that are not yet present in the minumum spanning tree. for (NodeCost pair_node_cost : graph.get(node)) int adj_node = pair_node_cost.node; if (added[adj_node] == false) pq.add(pair_node_cost); > > > > return mst_cost; > public static void main(String args[]) Prims p = new Prims(); int num_nodes = 6; // Nodes (0, 1, 2, 3, 4, 5) ListListNodeCost>> graph_1 = new ArrayList<>(num_nodes); for (int i=0; i num_nodes; i++) graph_1.add(new ArrayList<>()); > // Node 0 Collections.addAll(graph_1.get(0), new NodeCost(1, 4), new NodeCost(2, 1), new NodeCost(3, 5)); // Node 1 Collections.addAll(graph_1.get(1), new NodeCost(0, 4), new NodeCost(3, 2), new NodeCost(4, 3), new NodeCost(5, 3)); // Node 2 Collections.addAll(graph_1.get(2), new NodeCost(0, 1), new NodeCost(3, 2), new NodeCost(4, 8)); // Node 3 Collections.addAll(graph_1.get(3), new NodeCost(0, 5), new NodeCost(1, 2), new NodeCost(2, 2), new NodeCost(4, 1)); // Node 4 Collections.addAll(graph_1.get(4), new NodeCost(1, 3), new NodeCost(2, 8), new NodeCost(3, 1), new NodeCost(5, 4)); // Nod e 5 Collections.addAll(graph_1.get(5), new NodeCost(1, 3), new NodeCost(4, 4)); // Start adding nodes to minimum spanning tree with 0 as the souce node System.out.println("Cost of the minimum spanning tree in graph 1 : " + p.Find_MST(0, graph_1)); // Outgoing edges from the node: in graph 2. num_nodes = 7; // Nodes (0, 1, 2, 3, 4, 5, 6) ListListNodeCost>> graph_2 = new ArrayList<>(num_nodes); for (int i=0; i num_nodes; i++) graph_2.add(new ArrayList<>()); > // Node 0 Collections.addAll(graph_2.get(0), new NodeCost(1, 1), new NodeCost(2, 2), new NodeCost(3, 1), new NodeCost(4, 1), new NodeCost(5, 2), new NodeCost(6, 1)); // Node 1 Collections.addAll(graph_2.get(1), new NodeCost(0, 1), new NodeCost(2, 2), new NodeCost(6, 2)); // Node 2 Collections.addAll(graph_2.get(2), new NodeCost(0, 2), new NodeCost(1, 2), new NodeCost(3, 1)); // Node 3 Collections.addAll(graph_2.get(3), new NodeCost(0, 1), new NodeCost(2, 1), new NodeCost(4, 2)); // Node 4 Collections.addAll(graph_2.get(4), new NodeCost(0, 1), new NodeCost(3, 2), new NodeCost(5, 2)); // Node 5 Collections.addAll(graph_2.get(5), new NodeCost(0, 2), new NodeCost(4, 2), new NodeCost(6, 1)); // Node 6 Collections.addAll(graph_2.get(6), new NodeCost(0, 1), new NodeCost(1, 2), new NodeCost(5, 1)); // Start adding nodes to minimum spanning tree with 0 as the souce node System.out.println("Cost of the minimum spanning tree in graph 2 : " + p.Find_MST(0, graph_2)); > > Cost of the minimum spanning tree in graph 1 : 9 Cost of the minimum spanning tree in graph 2 : 6 Copyright (c) 2019-2023, Algotree.org. All rights reserved.
Алгоритм Прима с реализацией Java
В этом уроке мы сначала узнаем, что такое минимальные остовные деревья. После этого мы воспользуемся алгоритмом Прима, чтобы найти его.
2. Минимальное остовное дерево
Минимальное остовное дерево (MST) — это взвешенный неориентированный связный граф, общий вес ребер которого минимизирован за счет удаления более тяжелых ребер . Другими словами, мы сохраняем все вершины графа нетронутыми, но можем удалить некоторые ребра, чтобы сумма всех ребер была минимальной.
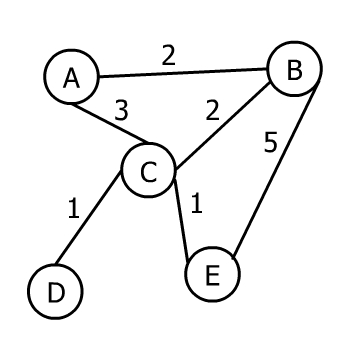
Начнем со взвешенного графа, так как нет смысла минимизировать общий вес ребер, если эти ребра вообще не имеют веса. Давайте посмотрим на пример графика:
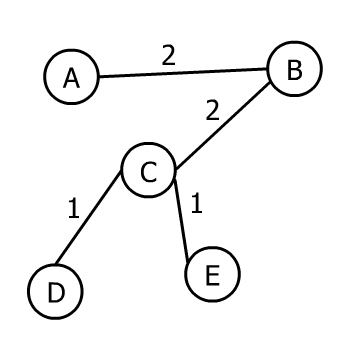
Приведенный выше граф является взвешенным неориентированным связным графом. Вот MST этого графика:
Однако MST графа не уникален. Если граф имеет более одного MST, то каждый MST имеет одинаковый общий вес ребра.
3. Алгоритм Прима
Алгоритм Прима принимает взвешенный неориентированный связный граф в качестве входных данных и возвращает MST этого графа в качестве выходных данных .
Работает жадно . На первом шаге он выбирает произвольную вершину. После этого каждый новый шаг добавляет ближайшую вершину к построенному дереву до тех пор , пока не останется несвязанной вершины.
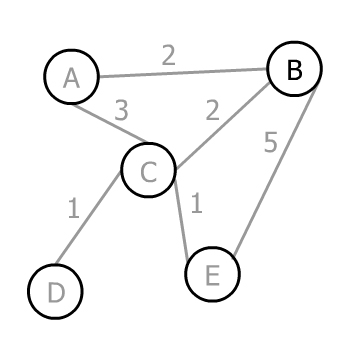
Давайте пошагово запустим алгоритм Прима на этом графе:
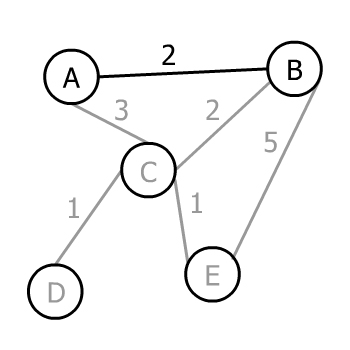
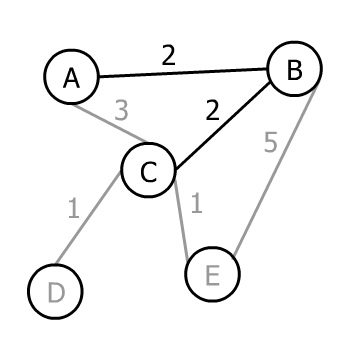
Предполагая, что произвольная вершина для запуска алгоритма — это B, у нас есть три варианта A, C и E. Соответствующие веса ребер равны 2, 2 и 5, поэтому минимум равен 2. В данном случае у нас есть два ребра весом 2, поэтому мы можем выбрать любое из них (неважно какое). Выберем А:
Теперь у нас есть дерево с двумя вершинами A и B. Мы можем выбрать любое из еще не добавленных ребер A или B, которые ведут к недобавленной вершине. Итак, мы можем выбрать AC, BC или BE.
Алгоритм Прима выбирает минимум, равный 2, или BC:
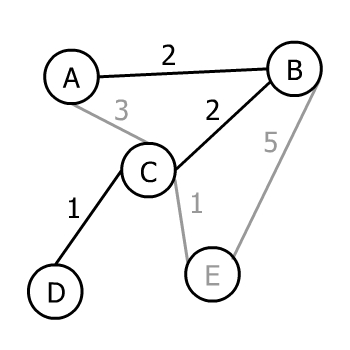
Теперь у нас есть дерево с тремя вершинами и тремя возможными ребрами для продвижения вперед: CD, CE или BE. AC не включен, так как он не добавит новую вершину в дерево. Минимальный вес среди этих трех равен 1.
Однако есть два ребра, каждое из которых имеет вес 1. Следовательно, алгоритм Прима выбирает одно из них (опять же не имеет значения, какое именно) на этом шаге:
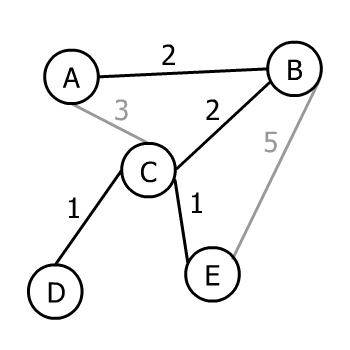
Осталась только одна вершина для соединения, поэтому мы можем выбрать из CE и BE. Минимальный вес, который может связать с ним наше дерево, равен 1, и его выберет алгоритм Прима:
Поскольку все вершины входного графа теперь присутствуют в выходном дереве, алгоритм Прима завершается. Следовательно, это дерево является MST входного графа.
4. Реализация
Вершины и ребра составляют графы, поэтому нам нужна структура данных для хранения этих элементов. Создадим класс Edge :
public class Edge private int weight; private boolean isIncluded = false; > Каждое ребро должно иметь вес , так как алгоритм Прима работает на взвешенных графах. isIncluded показывает, присутствует ли Edge в минимальном связующем дереве или нет.
Теперь добавим класс Vertex :
public class Vertex private String label = null; private MapVertex, Edge> edges = new HashMap>(); private boolean isVisited = false; > Каждая вершина может дополнительно иметь метку . Мы используем карту ребер для хранения соединений между вершинами. Наконец, isVisited показывает, посещалась ли до сих пор вершина алгоритмом Прима или нет.
Давайте создадим наш класс Prim , в котором мы реализуем логику:
public class Prim private ListVertex> graph; > Списка вершин достаточно для хранения всего графа, потому что внутри каждой вершины у нас есть Map для идентификации всех соединений. Внутри Prim мы создаем метод run() :
public void run() if (graph.size() > 0) graph.get(0).setVisited(true); > while (isDisconnected()) Edge nextMinimum = new Edge(Integer.MAX_VALUE); Vertex nextVertex = graph.get(0); for (Vertex vertex : graph) if (vertex.isVisited()) PairVertex, Edge> candidate = vertex.nextMinimum(); if (candidate.getValue().getWeight() nextMinimum.getWeight()) nextMinimum = candidate.getValue(); nextVertex = candidate.getKey(); > > > nextMinimum.setIncluded(true); nextVertex.setVisited(true); > > Начнем с установки первого элемента графа List как посещенного. Первым элементом может быть любая из вершин в зависимости от порядка их добавления в список в первую очередь. isDisconnected() возвращает true , если какая-либо вершина еще не посещена:
private boolean isDisconnected() for (Vertex vertex : graph) if (!vertex.isVisited()) return true; > > return false; > В то время как минимальное остовное дерево isDisconnected() , мы перебираем уже посещенные вершины и находим ребро с минимальным весом в качестве кандидата на следующую вершину:
public PairVertex, Edge> nextMinimum() Edge nextMinimum = new Edge(Integer.MAX_VALUE); Vertex nextVertex = this; IteratorMap.EntryVertex,Edge>> it = edges.entrySet() .iterator(); while (it.hasNext()) Map.EntryVertex,Edge> pair = it.next(); if (!pair.getKey().isVisited()) if (!pair.getValue().isIncluded()) if (pair.getValue().getWeight() nextMinimum.getWeight()) nextMinimum = pair.getValue(); nextVertex = pair.getKey(); > > > > return new Pair>(nextVertex, nextMinimum); > Мы находим минимум всех кандидатов в основном цикле и сохраняем его в nextVertex . Затем мы устанавливаем nextVertex как посещенный. Цикл продолжается до тех пор, пока не будут посещены все вершины.
В конце присутствует каждое ребро с параметром isIncluded , равным true .
Обратите внимание, что поскольку nextMinimum() выполняет итерацию по краям, временная сложность этой реализации составляет O(V 2 ) . Если вместо этого мы сохраним ребра в приоритетной очереди (отсортированной по весу), алгоритм будет выполняться за O(E log V) .
5. Тестирование
Итак, теперь, когда у нас есть код, давайте проверим его на реальном примере. Сначала построим наш график:
public static ListVertex> createGraph() ListVertex> graph = new ArrayList>(); Vertex a = new Vertex("A"); ... Vertex e = new Vertex("E"); Edge ab = new Edge(2); a.addEdge(b, ab); b.addEdge(a, ab); ... Edge ce = new Edge(1); c.addEdge(e, ce); e.addEdge(c, ce); graph.add(a); ... graph.add(e); return graph; > Конструктор класса Prim берет его и сохраняет внутри класса. Мы можем распечатать входной график с помощью метода originalGraphToString() :
Prim prim = new Prim(createGraph()); System.out.println(prim.originalGraphToString()); A --- 2 --- B A --- 3 --- C B --- 5 --- E B --- 2 --- C C --- 1 --- E C --- 1 --- D Теперь мы запускаем алгоритм Прима и печатаем полученный MST с помощью метода minimumSpanningTreeToString() :
prim.run(); prim.resetPrintHistory(); System.out.println(prim.minimumSpanningTreeToString()); Наконец, мы распечатываем наш MST:
A --- 2 --- B B --- 2 --- C C --- 1 --- E C --- 1 --- D 6. Заключение
В этой статье мы узнали, как алгоритм Прима находит минимальное остовное дерево графа. Код доступен на GitHub .